想必大家都记得上学时，很多老师都喜欢用1.01的365次方和0.99的365次方来论证要坚持每天进步，上班后可能老板也用这种方法鞭策过大家，提高大家的工作积极性。可这真的跟实际相符吗？今天来和大家聊聊。

01，1.01^365次方是啥样的曲线？

无聊的做了个图（每天坚持定量学习不是365次方而是365倍，所以老师论证是错误的）

所谓的1.01^365次方，曲线长得是这样子的：

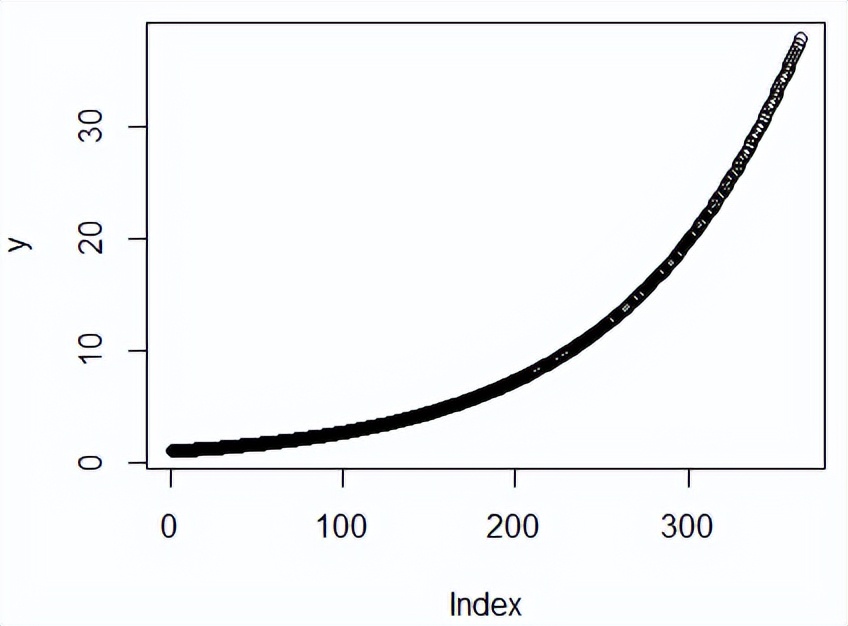
所以，你至少在很长一段时间内感觉不到那种飞一般的感觉。

02，从时间角度来量化1.01^365次方

纯粹按照时间来量化（因为容易量化）：那么假定一个人纯粹学习，除去睡觉，吃饭，上下课，去卫生间等，当然也包括你打盹，走神等时间，估计上限是12个小时左右，也就是720分钟。

那么，365天每天1.01的进步法，算了下，你的起步时间是19.05597分钟。

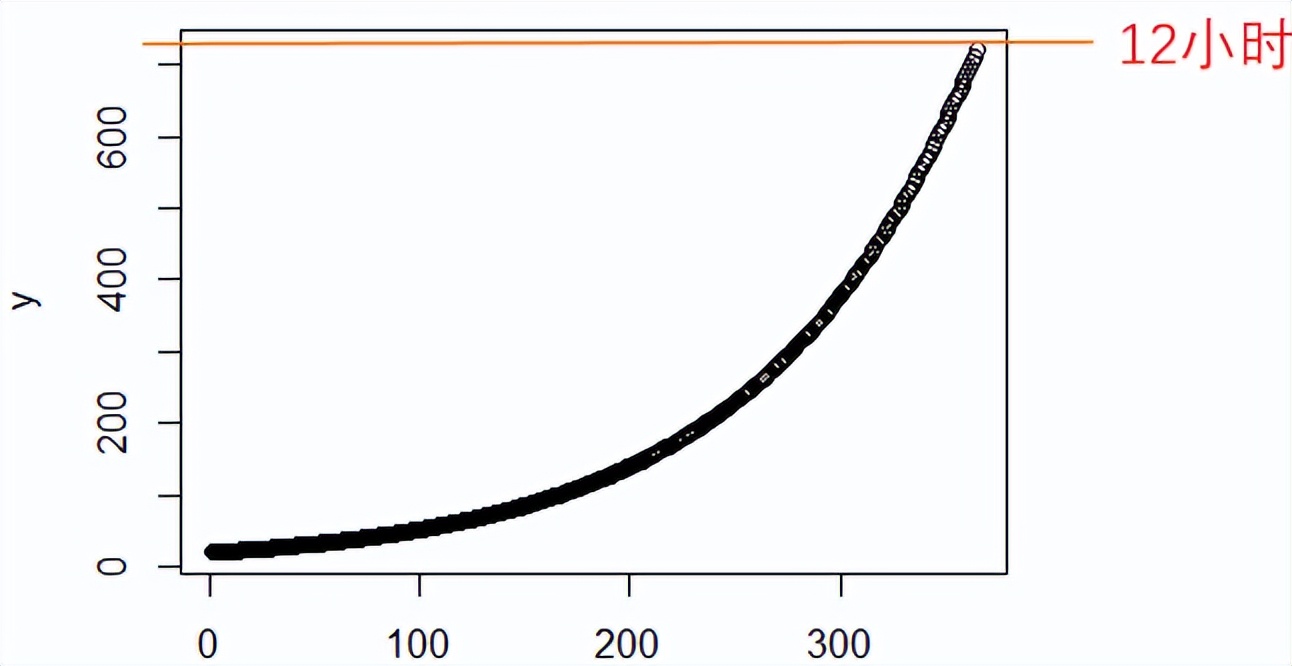
换句话，如果在这之前，你每天只学习19分钟多，然后接下来每天学习时间增加1%，你将在1年后学习时间达到12小时。

但是好景不长，接下来你继续按照每天增加1%去努力，那么你将在第434天的时候，学习时间达到24小时。

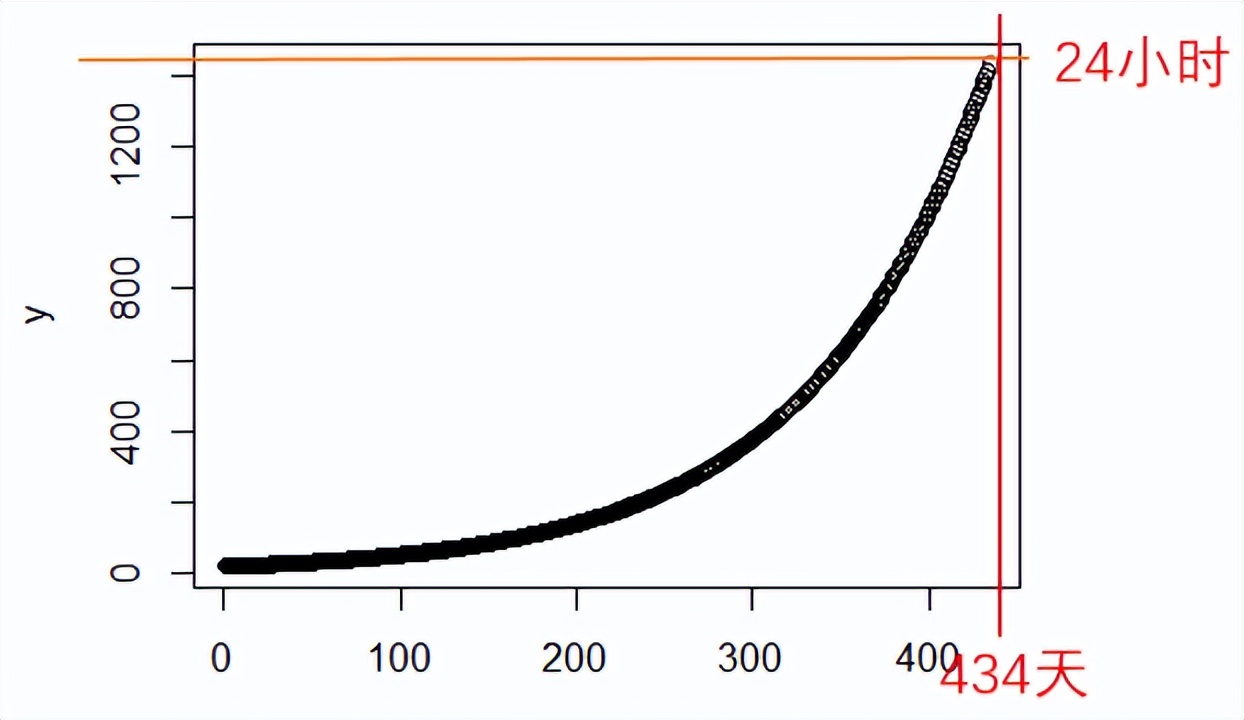
再往下，你只能换个星球（比如下图中的水星、金星、火星和冥王星一天时间就比较长）或者跑到黑洞去了，因为地球自转一天不到24小时。

所以，如果你之前每天学习19分钟，每天增加1%，365天后你的每天学习时间就是12小时，434天后你每天的学习时间就是24小时了，达到了地球自转周期的极限了。这时有的网友就说了，那我们把起点调低一点呢？下面把起点调低来论证。

03，起步低一点呢？

我们把起点调低，比如第一天学习1分钟，那么第一个365天后，你的数据是37.78343分钟；第二年730天后你的数据是1427.588分钟，已经是23.7833小时了，逼近地球自转周期。如果恰好碰到了闰年，很不幸，你的学习时间会变成 1441.864分钟，折合24.03106，超出了地球自转周期。

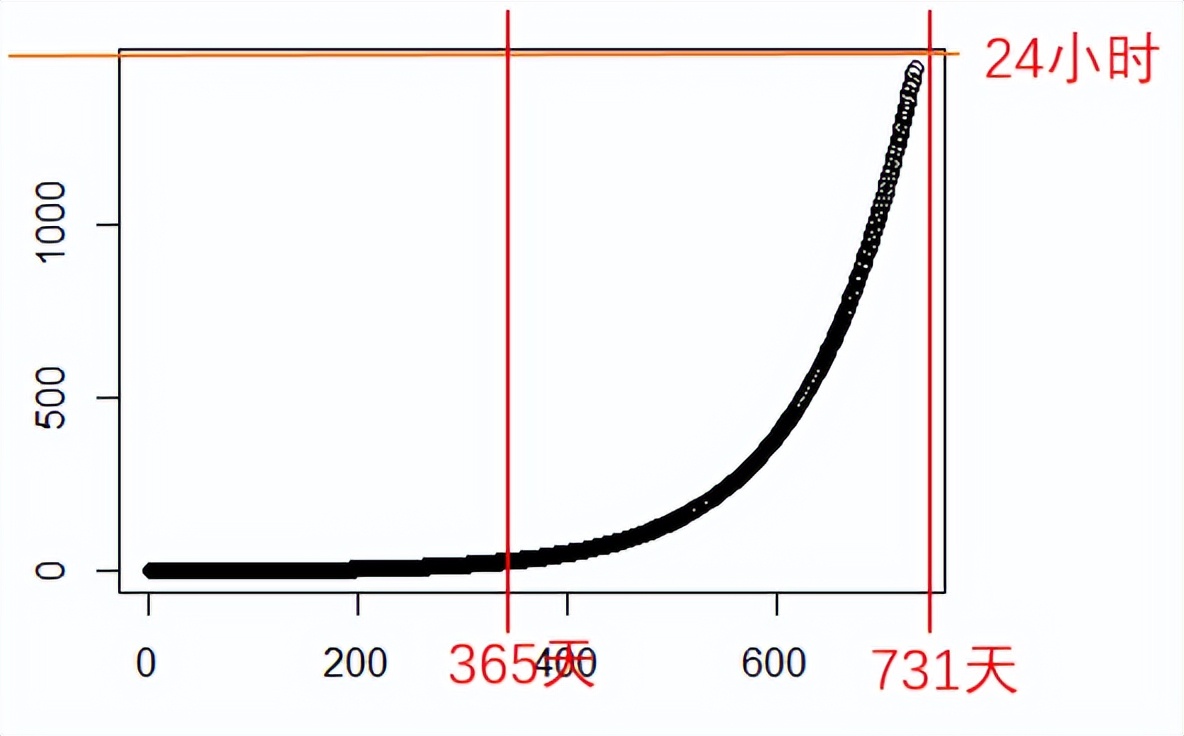
所以，时间上的1.01^365，不是那么容易实现的，这很大程度取决于你的起始时间，但即便是起始1分钟，两年后，你的学习时间已经突破地球极限了。

04，反过来，0.99的增速呢？

假定你开始是个学魔，一天除去吃喝拉撒打盹走神学习12小时，也就是720分钟，那么1年后，你只能学习18分钟了。

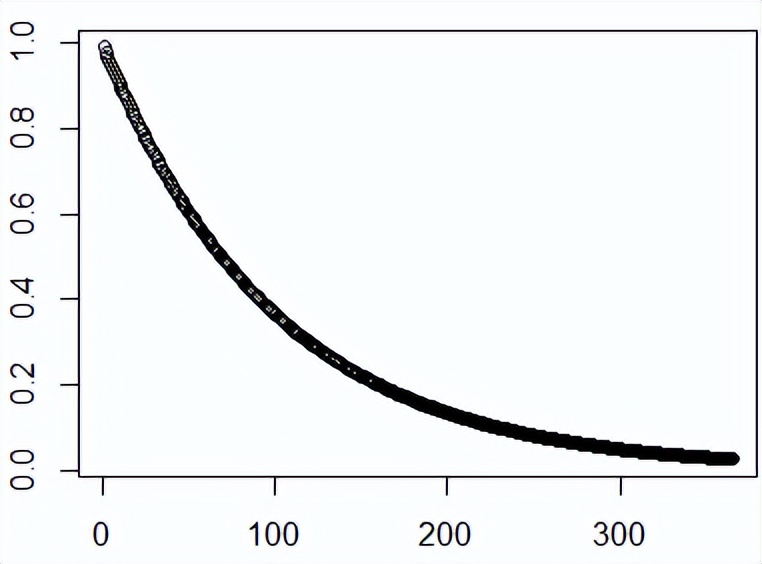
继续下去，你将在第654天，学习时间低于1分钟。

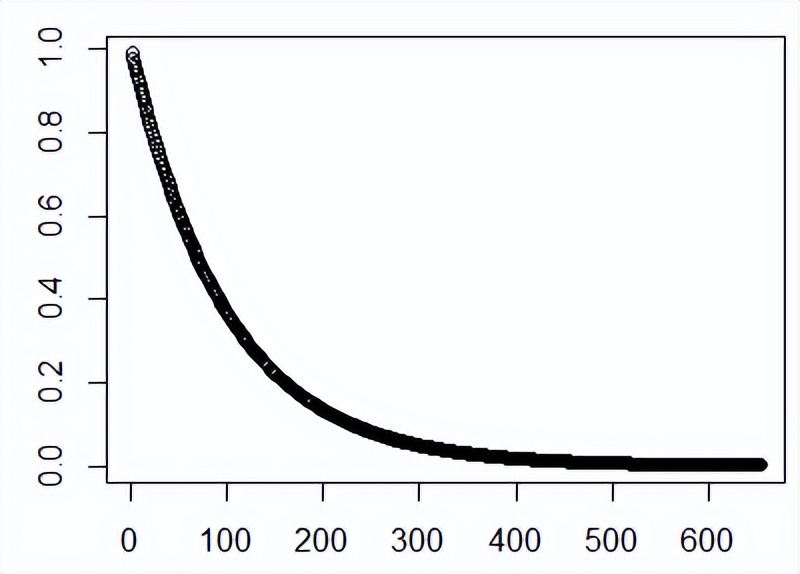
这种情况下，你基本上等于连老师好都不用喊了，退学在家了。至于学习效率之类的，就不好评价，不容易量化。

最后，至于很多人说的，每天坚持，这种不是次方算，而是倍数关系，比如“每天锻炼一小时，健康工作五十年，幸福生活一辈子”

来源: 李雷