数学中有很多面积公式，这些公式可以帮助我们快速地计算面积。例如，面积用S表示，长方形的面积公式为：S=ab(a表示长，b表示宽)；正方形的面积公式为：S=a²(a表示边长)；圆形的面积公式为：S=πr²（r表示半径）等等。这些都是比较规则的图形的面积公式，那么像一片枫叶这样的不规则形状，又该如何计算面积呢？

想要计算一片树叶的面积，我们需要利用一个标准的方格纸来测量。假如这个方格纸里的每一小格都是1平方厘米，当我们把树叶放在方格纸上时，可以数数它占了多少小格子，从而能得出这片树叶的面积。不过，当我们数小方格时会发现，并不是所有的小方格都被占了满格，这时我们要用“格点法”来解决。

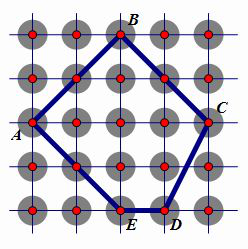
在一个由多条水平线和多条垂直线组成的方格图形上，如果任意相邻的两条平行线之间的距离都相等，我们就把这些平行线的交点称为格点，那么相邻两个格点的距离就是一个长度单位，四个格点组成的小正方形的面积就是一个面积单位。

如果一个多边形的顶点全是格点，这个多边形就叫做格点多边形。格点多边形的面积计算一般有三种方法：

1.规则格点多边形，比如正方形，可以用正方形的面积公式即：S=a²(a表示边长)来计算。

2.比较简单的格点多边形，例如上图，可以用数格子的方法来计算面积。上图中的格点多边形有5个完整的小正方形，6个小正方形一半面积的小三角形，1个占2个正方形一半面积的大三角形，所以上图中的格点多边形的面积为：5+6÷2+2÷2=9平方厘米。

3.比较复杂的格点多边形，就要用皮克公式计算。

皮克公式是乔治·亚历山大·皮克发现的，他为格点几何与微分几何做出了卓越贡献。皮克定理发表于1899年，任何一个格点多边形，只要数出多边形边界上的格点数以及图内的格点数，就可以用皮克公式算出这个格点多边形的面积。皮克公式即：S=a+b÷2-1（a表示图内格点的个数，b表示边界上的格点数）。所以，用皮克公式来计算上图中格点多边形的面积即：S=6+8÷2-1=9平方厘米。

由此，皮克公式确实能够准确地算出格点多边形或者不规则图形的面积，关于枫叶或者任何一种树叶的面积，大家都可以用皮克公式亲自算一算。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。