大家都知道汽车前照灯发出的光可以照亮车体前方的路况，使驾驶者可以在漆黑的夜晚安全地行车，保证视野清晰。但是你是否知道汽车前灯可以由亮转暗和照射距离的变化，都是应用到了数学原理呢？

如果你留心便会发现，汽车前灯后面的反射镜呈抛物线的形状。把抛物线沿它的对称轴旋转一周，就会形成一个抛物面，这种抛物面形状，正是我们熟悉的汽车前灯的反射镜形状，这种形状使车灯既能够发出明亮的、照射很远的平行光束，又能发出较暗的、照射近距离的光线。

我们都知道常规的前照灯主要是由灯泡、反射镜和透镜三部分组成。明亮的光束，是由位于抛物面形状反射镜焦点的光源射出的，灯泡位于抛物面的焦点上，灯泡发出的光经抛物面反射镜反射形成平行光束，再经过配光镜的散射、偏转作用，以达到照亮路面的效果，这样的灯光我们通常称为远光灯；而较暗的光线，不是由反射镜焦点的光源射出的，光线的行进与抛物线的对称轴不平行，光线只能向上和向下照射，所以照射距离并不远，如果把向上射出的光线遮住，车灯就只能发出向下的、射的很近的光线了。

由上面所知，汽车大灯反射镜射出的灯光是平行光束，接下来我们就用数学原理来证明它的正确性。

证明：

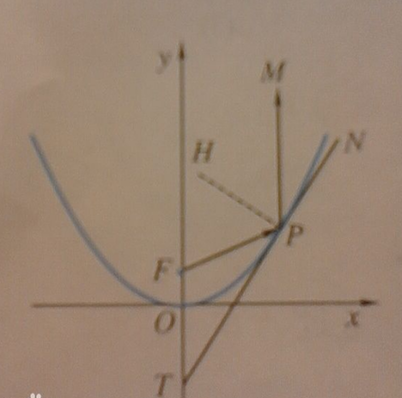
设P（x0，y0），PT是抛物线在P处的切线，PH⊥PT，抛物线的方程为：

(a>0)，焦点F坐标为（0，  ）

根据抛物线的定义知

又抛物线导数为 

所以切线PN的斜率为2ax0，方程为y-y0=2ax0(x-x0)

求点T的坐标，令x=0，联立抛物线方程得

则点T坐标为（0，-y0）所以

所以PF=FT，∠FTP=∠FPT，

又∠FPT=∠MPN

所以∠FTP=∠MPN

MP平行于y轴

通过上面的数学证明，我们可以知道汽车前灯的反光曲面与轴截面的交线是抛物线，由抛物线的性质可知，经过反射镜的反射，能够沿着与抛物线的对称轴平行的方向发射出去平行光线，反之，与抛物线的轴平行的光线经旋转抛物面反射后，都聚集到抛物线的焦点上，这就是抛物线的光学性质，它被广泛应用于探照灯、汽车前灯、抛物面天线等地方。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。