古希腊数学家丢番图的墓碑上写道：“过路人，这座石墓里安葬着丢番图。他生命的1/6是幸福的童年，生命的1/12是青少年时期。又过了生命的1/7他才结婚。婚后5年有了一个孩子，孩子活到他父亲一半的年纪便死去了。孩子死后，丢番图在深深的悲哀中又活了4年，也结束了尘世生涯。过路人，你知道丢番图的年纪吗？”长眠于如此奇特的墓志铭之下，丢番图对于数学的热爱可见一斑。那么，丢番图在数学上有怎样的成就？他究竟活了多大年纪呢？

丢番图是古希腊著名的数学家，他是代数学的创始人之一，对算术理论有着深入的研究。丢番图认为代数方法比几何的演绎陈述更适宜于解决问题，而他在解题的过程中显示出的巧思和独创性，在希腊数学中独树一帜，因此被后人称为“代数学之父”。亚历山大时期的丢番图对代数学的发展起了极其重要的作用，对后来的数论学者有很深的影响。古代数学名著《算术》就是丢番图的著作，也是他的重要成就。

《算术》讲的是数的理论，但大部分内容可以划入代数的范围。它的特点是完全脱离了几何的形式，并且创用了一套缩写符号，如未知量、未知量的各次幂等都用特殊符号来表示。在这以前，人们都是使用文字来叙述问题的，丢番图创用的这些缩写符号，可以说是代数符号的起源了。虽然这些记号还只是缩写性质，但这是真正符号代数出现之前的一个重要阶段，这在代数发展史上是一个巨大的进步。丢番图的《算术》还特别以不定方程的求解而著称。所谓“不定方程”，是指未知数个数多于方程个数的代数方程（组），它是数论的一个分支。丢番图是第一个对不定方程问题做了广泛、深入研究的数学家，因此，直到今天，我们常常把求整系数不定方程的整数解的问题叫“丢番图问题”或“丢番图分析”，而将不定方程称之为“丢番图方程”。

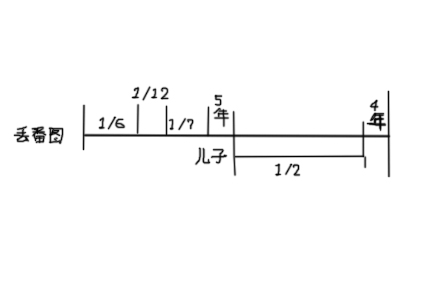
其实，丢番图最为人乐道的不是他的数学成就，而是他那奇特的墓志铭。他的墓志铭便是一组求解他年龄的方程，我们假设丢番图活了x岁,可得：

1/6x+1/12x+1/7x+5+1/2x+4=x

14/84x+7/84x+12/84x+42/84x+9=x

75/84x+9=x

x-75/84x=9

9/84x=9

x=84

所以，代数学之父丢番图活了84岁，他33岁结婚，38岁生子，孩子仅陪伴了他42年，4年后他走完了一生，留下了令人称奇的墓志铭。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。