在数学中，对数是对求幂的逆运算，正如除法是乘法的倒数，反之亦然。 这意味着一个数字的对数是必须产生另一个固定数字（基数）的指数。 “对数”一词是苏格兰数学家纳皮尔首先创造的，意思是“比数”。对数的重要性可以用伽利略的一句话来体现：“给我空间、时间及对数，我就可以创造一个宇宙！”

十六世纪中期，瑞士钟表匠标尔基不仅精通钟表修理，还会修理天文仪器。他结识天文学家开普勒后，发现开普勒每天与天文数字打交道，由于数字很大，计算量非常繁重。于是标尔基产生了简化计算的思想，因此可以说最早研究“对数”的就是标尔基。

构造对数表的主要困难在于取什么数作底数。把底数取大一点就会出现：对数每增加万分之一，真数就增加十倍，真数变化太快，会导致真数表不好用。最后经过反复演算，标尔基取的底数是，他发现这样的底数可以使对数和真数变化速度差不多。虽然标尔基是历史上第一位研究“对数”的人，但是真正使“对数”广泛流传的却是纳皮尔。

纳皮尔在1614年出版了《奇妙的对数定律说明书》，书中借助运动学，用几何术语阐述了对数方法，书中取的对数的底数是。这个数表的出版震惊了数学界，许多人对这个表很感兴趣，其中就包括英国牛津大学数学天文学教授布里格斯。1616年布里格斯访问纳皮尔，他建议为了实用方便，可以把对数的底由改为，因为以10为底在数值计算上更具优越性。然而，第二年纳皮尔就去世了，于是布里格斯与荷兰数学家弗拉寇合作，利用10年时间计算出了从1到20000和从90000到100000，以10为底的14位的对数表，之后，弗拉寇又补充了从20000到90000的对数表。

布里格斯的对数表便是现在四位常用对数表的先驱。法国著名数学家和天文学家拉普拉斯说：“对数的算法，不仅免除大数计算时不易避免的错误，并且数月的工作可用数天完成，这就相当于延长了天文学家的生命”。

我们可以看看布里格斯的工作量是相当大的！以计算为例：

……

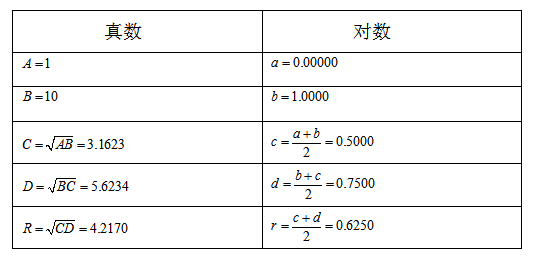
依次递进，进行22次开方，求出真数约为0.5000，其相应对数为0.69990。

实际上对数的发现要早于指数，在没有计算机、计算器的时候，我们学习对数都离不开常用对数表，它的出现无论是在数学领域还是在天文领域都发挥了重要作用。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。