关于复变量s=σ+jω的有理函数G(s)=N(s)/D(s)为严格正实函数，如果有：(1)当s为实数时，只要G(s)有定义，它就是实函数；(2)G(s)在右半闭平面上没有极点；(3)ReG(jω)>0，对于-∞0上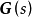，的每个元素都是解析的，即每个元素在Res>0上没有极点；

　　(2)对于所有的Res>0的s，矩阵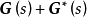便是半正定的Hermite矩阵。

　　严格正实函数矩阵

　　实有理函数方阵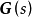是严格正实函数矩阵。如果：

　　(1)往右半闭平面Res≥0上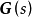，的每个元素都是解析的；

　　(2)对于所有的Res≥0的s，矩阵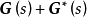便是半正定的Hermite矩阵。

　　本词条内容贡献者为:

　　李岳阳 - 副教授 - 江南大学

严格正实函数

图文简介