若在最初博弈中，第二个集合由一个孤立的玩家组成，它也被称为一个“哑玩家”。

　　简介

　　若在第二个集合由一个孤立的玩家组成，它也被称为一个“哑玩家”。这暗示着对博弈的另一种推广：一个博弈，其中参与者落入两个集合，第一个集合中的参与者严格地在其内部进行一个博弈，而第二个集合中的参与者对该博弈中它们自己的命运和其他玩家的命运都没有任何影响，那么，这些玩家是哑玩家。1

　　定义

　　给一个博弈添加“哑玩家”。

　　考虑玩家1’，…，k’的博弈△。通过添加一系列“哑玩家”K使其“膨胀”，即将△与玩家1’’，....,l’’的一个非本质博弈H合成。那么，这个合成博弈是r。

　　这一结果能够被总结为：通过添加“哑玩家”，一个博弈的“膨胀”基本上不影响其解——没有必要给每个分配添加代表“哑玩家”的分量，而且这些分量的值是显然的：每个“哑玩家”在非本质博弈H中本可以得到的数额，这描述了它们的相互关系。

　　最后，当且仅当合成不是上述特殊类型的合成时，旧理论才不具有新理论的简单性质，而且，其遗传性也消失。

　　因此，W恰好由这样一些S组成：除(n)或(n—1，n)之外，所有包含n的集合；除(1，…，n—1)和(1，…，n—2)之外的不包含n的集合。

　　换句话说：该博弈的核是一个(n—1)人博弈，其参与者是1，…，n—2，n，其W由(1，n)，…，(n—2，n)，(1，…，n—2)组成。因此，这是n—1位玩家时的情况C。-：，类似于n位玩家时的情况C。—：(用n—1替换n!)。所以，它有记号[1，…，l，n—3]k。玩家n—1是一个“哑玩家”。

　　情况Cn…2恰好由一个博弈代表：①有一个哑玩家的(n—1)人博弈[1，，…，l，n—3]k。

　　(有哑玩家的)不同于[1，…，l，，l-2]，的简单博弈：Ck,k=0，1,....,n-3

　　如果n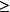4，那么，我们能够通过对任一l=3，…，n建立[1,，…，l，l-2]k，并加上必要个数的哑玩家来得到一个简单n人博弈。

　　我们将这一结论重述为： 我们希望枚举n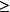4的全部n人博弈。 博弈[1，…，1，l—2]。(l位玩家)加上(n—l)

　　个“哑玩家”是一个简单n人博弈，l=3，4，…，n。其情况分别是C·，C3，，…，Cm-1。其他简单n人博弈(如果有的话)属于情况C。，C1 .....Cn-3。2

　　本词条内容贡献者为:

　　王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所