对于巴拿赫空间的闭凸集A，毕晓普-费尔泼斯定理断言：A的支撑点在A的边界中稠密。

简介

对于巴拿赫空间的闭凸集A，毕晓普-费尔泼斯定理断言：A的支撑点在A的边界中稠密。1

超平面的支撑点

设A是实线性空间X的集合，a∈A。如果超平面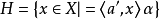对于任何y∈A满足≥=α，那么H称为A的支撑超平面，a也称为H的支撑点。

相对于代数内部非空的凸集的代数边界点都可称为支撑该凸集的超平面的支撑点。

代数边界

（algebraic boundary）

代数边界是实线性空间中的集合的代数意义下的边界。

它是集合的代数闭包去掉其嗲数内部后所形成的集合。也就是说，它是当实线性空间X以代数开集为开集时的拓扑意义下的边界。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学

毕晓普-费尔泼斯定理

图文简介

对于巴拿赫空间的闭凸集A，毕晓普-费尔泼斯定理断言：A的支撑点在A的边界中稠密。