共轭丛(conjugate bundle)是与复向量丛相关且有相互复结构的向量丛。
简介共轭丛是与复向量丛相关且有相互复结构的向量丛。
若ω 是一个复向量丛,共轭丛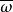 是一个复向量丛,与ω有相同的基本实向量丛
是一个复向量丛,与ω有相同的基本实向量丛
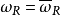 但有“相反的”复结构,因而映射
但有“相反的”复结构,因而映射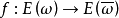 是共轭线性的,即对每个复数λ 及每个
是共轭线性的,即对每个复数λ 及每个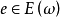 ,有
,有
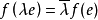 其中
其中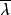 是
是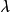 的共轭复数。1
的共轭复数。1
共轭丛的陈类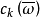 等于
等于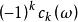 ,因而
,因而
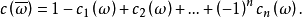
向量丛是一个几何构造,对于拓扑空间(或流形,或代数簇)的每一点用互相兼容的方式附上一个向量空间,所用这些向量空间"粘起来"就构成了一个新的拓扑空间(或流形,或代数簇)。
一个典型的例子是流形的切丛:对流形的每一点附上流形在该点的切空间。或者考虑一个平面上的光滑曲线,然后在曲线的每一点附上和曲线垂直的直线;这就是曲线的"法丛"。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所

 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助