全陈类(total Chern class)是各阶陈类之和。陈类是复向量丛的一种上同调类。
简介全陈类是各阶陈类之和。
环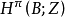 中形式和式
中形式和式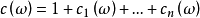 就称为ω的全陈类,其中
就称为ω的全陈类,其中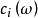 为复n维向量丛ω 的第 i 个陈类。1
为复n维向量丛ω 的第 i 个陈类。1
陈类是复向量丛的一种上同调类。
设ω为复 n 维向量丛,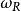 为其基本实向量丛,
为其基本实向量丛,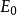 表
表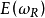 中所有非零向量所成子空间,
中所有非零向量所成子空间,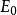 中任意点 v 位于ω 的一个确定的纤维
中任意点 v 位于ω 的一个确定的纤维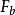 中,设ω 上给定埃尔米特度量,取 v 在
中,设ω 上给定埃尔米特度量,取 v 在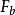 中的正交补作为点 v 上的纤维,得以
中的正交补作为点 v 上的纤维,得以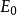 为底空间的复 n-1 维向量丛
为底空间的复 n-1 维向量丛 ,则陈类
,则陈类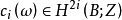 按ω 的复维数递推地定义为:顶陈类(即最高维陈类)
按ω 的复维数递推地定义为:顶陈类(即最高维陈类)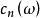 等于欧拉类
等于欧拉类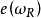 ;对
;对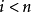 ,定义为
,定义为
 对
对 ,类
,类 。
。
若ω与𝝓是仿紧底空间B上的两个复向量丛,则惠特尼ω⨁𝝓的全陈类有下述公式:c(ω⨁𝝓)=c(ω)·c(𝝓),这被称为陈类的乘积公式。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所

 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助