n标架是线性无关向量的一个n元组，所有n标架的全体构成n重直积 的一个开子集。

简介格拉斯曼流形

格拉斯曼流形是与欧式空间相关的一种特殊流形，格拉斯曼流形 是通过坐标空间 的原点的所有 n 维平面的集合，这可以视为一个商空间。

定义

的一个 n 标架是 中线性无关向量的一个 n 元组， 中的所有 n 标架的全体构成 n重直积 的一个开子集，称其为施蒂费尔流形。

性质

有一个标准映射

它把每个n标架映为它所生成的n平面，给 以商拓扑如下：子集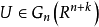 是开集的充分必要条件是 q 的逆映射的像 是开集。1

线性无关

线性独立一般是指向量的线性独立，指一组向量中任意一个向量都不能由其它几个向量线性表示。

特别地，所谓“线性关系”的本质就是“独立关系”（又叫线性独立）。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

n标架

图文简介

n标架是线性无关向量的一个n元组，所有n标架的全体构成n重直积 的一个开子集。