格拉斯曼流形（Stiefel manifold）是通过坐标空间的原点的所有 n 维平面的集合，这可以视为一个商空间。

简介

格拉斯曼流形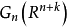是通过坐标空间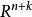的原点的所有 n 维平面的集合，这可以视为一个商空间。

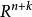的一个 n 标架是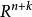中线性无关向量的一个 n 元组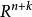，中的所有 n 标架的全体构成 n重直积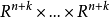的一个开子集，称其为施蒂费尔流形。

性质

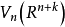格拉斯曼流形有一个标准映射

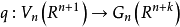它把每个n标架映为它所生成的n平面，给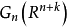以商拓扑如下：子集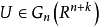是开集的充分必要条件是 q 的逆映射的像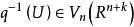是开集。

格拉斯曼流形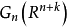是nk维紧光滑流形。1

商空间

（quotient space）

在线性代数中，一个向量空间V被一个子空间N的商是将N“坍塌”为零得到的向量空间，所得的空间称为商空间，记作V/N（读作V模N）。

设V是域K上的一个向量空间，且N是V的一个子空间。我们定义在V上定义一个等价类，如果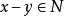则令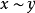。即如果其中一个加上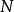中一个元素得到另一个，则与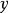相关。的所在等价类通常记作

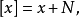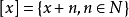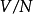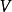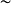因为它由给出。那么商空间定义为/，V在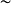下所有等价类集合。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

施蒂费尔流形

图文简介

格拉斯曼流形（Stiefel manifold）是通过坐标空间的原点的所有 n 维平面的集合，这可以视为一个商空间。