列维-辛钦公式（Levi-Khinchin formula）是描述群X与其对偶群关系的一个重要论断。

简介

列维-辛钦公式是描述群X与其对偶群关系的一个重要论断。

X的对偶群Γ上的一个复值函数ψ是一个具有对称列维测度的连续负定函数的充分必要条件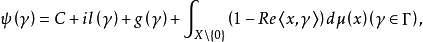其中常数C≥0，l是Γ的连续实值同态，g是Γ上非负连续二次型，μ是X\{0}上的正对称测度且满足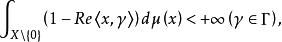并且，C,l,g,μ由ψ惟一决定，即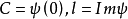，μ是关于ψ的列维测度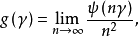，上述方程称为列维-辛钦公式。1

列维测度

列维测度是在X\{0}上与(μt)t>0相关联的一个正测度。

设(μt)t>0是X上的卷积半群，则在X\{0}上的正测度网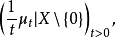当t→0时浑收敛于X\{0}上的一个正测度μ，称μ是关于(μt)t>0的列维测度。

对偶群

若G是局部紧致阿贝尔群，G的特征标是一个从G到圆群T的连续群同态；特征标在逐点乘法下构成一个群，一个特征标的逆元是它的复共轭。可证明所有G上的特征标在紧致开拓扑（即：以紧集上的一致收敛定义收敛性）下构成一个局部紧致阿贝尔群，称作对偶群。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

列维-辛钦公式

图文简介

列维-辛钦公式（Levi-Khinchin formula）是描述群X与其对偶群关系的一个重要论断。