列维测度（Levi measure）是在X\{0}上与(μt)t>0相关联的一个正测度。

简介

列维测度是在X\{0}上与(μt)t>0相关联的一个正测度。

设(μt)t>0是X上的卷积半群，则在X\{0}上的正测度网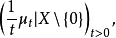当t→0时浑收敛于X\{0}上的一个正测度μ，称μ是关于(μt)t>0的列维测度。1

正测度

(positive measure)

正测度是仅在（环的）零元素上取值为零的测度。

设μ是定义在环上的测度，若μ的值只在零元素上为零，则称μ是一个正测度。

卷积半群

卷积半群是一种半群。

设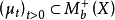满足如下条件：

1、∀t>0，μt(X)≤1；

2、∀t,s>0，μt∗μs=μt+s；

3、，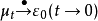

则称测度族(μt)t>0是X上的一个浑连续卷积半群。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学

列维测度

图文简介

列维测度（Levi measure）是在X\{0}上与(μt)t>0相关联的一个正测度。