迁移卷积半群是浑积分存在的卷积半群。若(μt)t>0不是迁移的，则称它为X上的常返卷积半群。

简介迁移卷积半群

迁移卷积半群是浑积分存在的卷积半群。

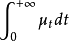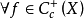设(μt)t>0是卷积半群，若(μt)t>0的浑积分存在，即对，均有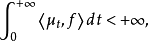则(μt)t>0称为X上的迁移卷积半群或非常返半群，这时有。

定义

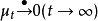若(μt)t>0不是迁移的，则称它为X上的常返卷积半群。1

卷积半群

卷积半群是一种半群。

设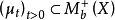满足如下条件：

1、∀t>0，μt(X)≤1；

2、∀t,s>0，μt∗μs=μt+s；

3、，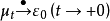

则称测度族(μt)t>0是X上的一个浑连续卷积半群。

浑积分

浑拓扑是一种特殊拓扑，在M(X)上用浑收敛定义的拓扑称为浑拓扑。

M(X)中的测度网(μα)α∈A，称为浑收敛于μ∈M(X)，记为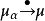，指的是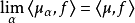对任意f∈Cc(x)成立。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

常返卷积半群

图文简介

迁移卷积半群是浑积分存在的卷积半群。若(μt)t>0不是迁移的，则称它为X上的常返卷积半群。