解析容量为零的集称为班勒卫零集（paineve null-set），又称为解析零容集。

简介解析容量

解析容量是定义在复平面的紧子集族上的一个集函数，其值由一族有界解析函数的导数来确定。

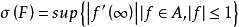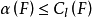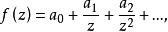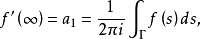设F为复平面C上的紧集，𝒜为C\F的非有界分支D∞上的有界复解析函数全体，称为F的解析容量。若用Cl(F)表示F的对数容量，则一般有。若将f在∞的邻域展开：则其中Γ是分离F与∞的闭曲线。

定义

解析容量为零的集称为班勒卫零集，又称为解析零容集。1

集函数

集函数是测度论中定义的概念，是以集类为定义域的函数。

设𝒞是Ω上的一个集类，K是实数域或复数域，称映射μ:𝒞→K为定义在𝒞上的集函数。重要的（数值）集函数有测度、集上的积分等。若实值集函数的值可允许取+∞或-∞，则称此集函数为扩充实值集函数。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

班勒卫零集

图文简介

解析容量为零的集称为班勒卫零集（paineve null-set），又称为解析零容集。