若Ω\E在E的每一点都瘦,则称E为肥集。E是细开集当且当E是肥集。
简介瘦性瘦性是描述一个点集在某一点的邻域充分“稀薄”的一个概念。
在拓扑空间(Ω,𝒥)中,取定一族从(Ω,𝒥)到(0,+∞)的下半连续函数组成的凸锥Φ,Ω的子集E称为在x0∉E瘦,指的是x0∉Ē(𝒥闭包),或x0∉Ē但存在u∈Φ,使得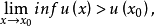 其x∈E。进一步,称E在x0(x0∈E)瘦,指的是E\{x0}在x0瘦且E在x0弱瘦。称E在任一点x0弱瘦,当且仅当对f≡1关于Φ的扫除函数
其x∈E。进一步,称E在x0(x0∈E)瘦,指的是E\{x0}在x0瘦且E在x0弱瘦。称E在任一点x0弱瘦,当且仅当对f≡1关于Φ的扫除函数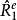 ,有inf{(
,有inf{(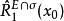 |σ为x0的邻域}
|σ为x0的邻域}
版权归原作者所有,如有侵权,请联系我们
若Ω\E在E的每一点都瘦,则称E为肥集。E是细开集当且当E是肥集。
简介瘦性瘦性是描述一个点集在某一点的邻域充分“稀薄”的一个概念。
在拓扑空间(Ω,𝒥)中,取定一族从(Ω,𝒥)到(0,+∞)的下半连续函数组成的凸锥Φ,Ω的子集E称为在x0∉E瘦,指的是x0∉Ē(𝒥闭包),或x0∉Ē但存在u∈Φ,使得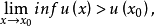 其x∈E。进一步,称E在x0(x0∈E)瘦,指的是E\{x0}在x0瘦且E在x0弱瘦。称E在任一点x0弱瘦,当且仅当对f≡1关于Φ的扫除函数
其x∈E。进一步,称E在x0(x0∈E)瘦,指的是E\{x0}在x0瘦且E在x0弱瘦。称E在任一点x0弱瘦,当且仅当对f≡1关于Φ的扫除函数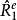 ,有inf{(
,有inf{(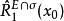 |σ为x0的邻域}
|σ为x0的邻域}