德拉姆同态是联系微分流形 M 上的德拉姆上同调群与奇异上同调群的一个自然同态。

简介概述

德拉姆同态是联系微分流形 M 上的德拉姆上同调群与奇异上同调群的一个自然同态，建立这个同态的关键是流形上的斯托克斯公式。

具体内容

设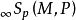 是它的对偶，即其中的每一个元素是M上一切可微奇异p单形到R的一个映射 f，这样的f称为M上的可微奇异p上链，令

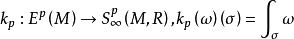其中ω为M上的p形式，σ是M中的可微奇异p单形，则由斯托克斯定理，

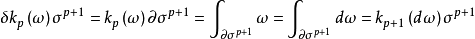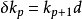即，其中 d 为外微分 ，δ 为奇异上链群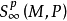中的上边缘运输，这表示同态族 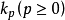与上边缘运输，d,δ 可交换，因此诱导上同调群之间的同态

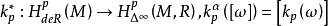这个同态称为德拉姆同态。1

德拉姆上同调群

(de Rham cohomology group)

德拉姆上同调群是闭形式空间关于正合形式空间的商。设M是微分流形，称闭p形式的实向量空间关于正合p形式子空间的商空间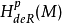：={闭p形式}/{正合p形式}为M的p维德拉姆上同调群。

这是1930年由德拉姆(de Rham，G.-W.)给出的，他建立了微分流形的微分结构与拓扑结构的一个重要关系。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

德拉姆同态

图文简介

德拉姆同态是联系微分流形 M 上的德拉姆上同调群与奇异上同调群的一个自然同态。