切纤维丛(tangent fiber bundle)是E流形上的每一点切空间的并所组成的纤维丛。
简介切纤维丛是E流形上的每一点切空间的并所组成的纤维丛。
设 X 是有图册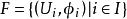 的E流形,令
的E流形,令
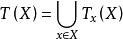
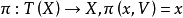 ,关于
,关于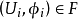 ,令
,令
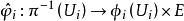
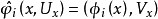 其中
其中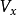 是
是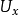 在
在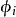 之下的代表,则容易验证,含
之下的代表,则容易验证,含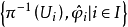 的最大图册,构成 T(X)的一个图册,在此图册之下,T(X)成为模型在 E×E内的
的最大图册,构成 T(X)的一个图册,在此图册之下,T(X)成为模型在 E×E内的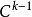 流形,成为 E 流形X的切丛。
流形,成为 E 流形X的切丛。
另一方面,丛纤维丛的角度,把一切与T(X)有关的对象集中于一起,可以写为(T(X),X,π,E,GL(E)),它是一个纤维丛,以T(X) 为全空间,X为底空间,E为典型纤维以及GL(E) 为结构群。
性质若 v 是切纤维丛T(X)的一个截面,即映射
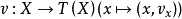 使得
使得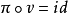 ,则 v 称为X上的向量场。1
,则 v 称为X上的向量场。1
纤维丛的理论,是1946年由美国的斯丁路特、美籍华人陈省身、法国的艾勒斯曼共同提出的。
数学上,特别是在拓扑学中,一个纤维丛(fiber/fibre bundle)是一个局部看来像两个空间的直积(特指笛卡尔积)的空间,但是整体可以有与直积空间不同的拓扑结构。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所

 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助