所谓无限维流形,通常是指巴拿赫空间或希尔伯特空间维模型空间的微分流形。
简介无限维流形是有限维流形的推广。
所谓无限维流形,通常是指巴拿赫空间或希尔伯特空间维模型空间的微分流形。
应用定义图册无限维流形为了适应数学研究的需要而发展起来的,除了它在维数等方面有别于普通的微分流形之外,很多概念都可以类似于有限维情形而获得定义,例如,可以定义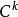 类图册。
类图册。
设 X 是一个集合,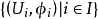 是一族区图集,若他满足下列条件,则称这样的
是一族区图集,若他满足下列条件,则称这样的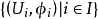 维一个
维一个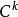 类图册,而每个
类图册,而每个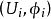 称为该图册中的区图:
称为该图册中的区图:
1、每个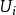 是 X 的一个子集,且
是 X 的一个子集,且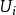 的全体覆盖 X;
的全体覆盖 X;
2、每个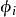 是
是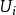 到某个巴拿赫空间 E 的开子集
到某个巴拿赫空间 E 的开子集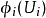 的双射,且对任意 i,j,
的双射,且对任意 i,j,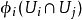 在E 中是开子集;
在E 中是开子集;
3、映射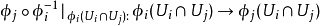 对每一对指标 i,j 是一个
对每一对指标 i,j 是一个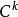 同构
同构
无限维流形也可以定义切向量:
设X是一个E流形,则在任一点 x∈X 处的切向量有两个等价的定义:
1、在流形 X 处的切向量是在x处相切的曲线的一个等价类,即所有的曲线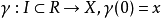 ,若在某个区图
,若在某个区图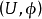 中,
中,
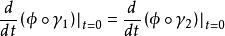 则称
则称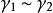 ,从而形成等价类,若向量
,从而形成等价类,若向量
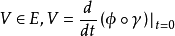 则称它为在区图
则称它为在区图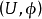 中在x处切于曲线γ 的切向量的代表;
中在x处切于曲线γ 的切向量的代表;
2、是x∈X 处三元组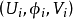 的等价类,其中
的等价类,其中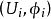 是 X 在 x 处的任一相容区图,
是 X 在 x 处的任一相容区图,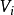 是 E 的一个向量,若
是 E 的一个向量,若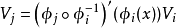 ,则三元组
,则三元组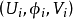 与
与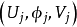 等价。
等价。
X在x处切向量的全体构成一个向量空间,称这个向量空间为切空间,记为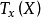 ,类似地也可定义相应的余切向量与余切空间
,类似地也可定义相应的余切向量与余切空间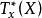 。1
。1
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所

 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助