维纳判别法（Wiener criterion）是波莱尔集E的边界点x0为E的α非正则点的充分必要条件。

简介

维纳判别法是边界点为α非正则点的判别准则。1

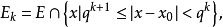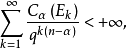维纳判别法如下：波莱尔集E的边界点x0为E的α非正则点的充分必要条件是，对于q∈(0,1)及有其中Cα表示α容量。这里Ek也可改为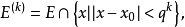也可把级数式改为积分式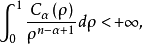其中

α非正则点

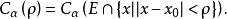
α正则点是位势论的一个概念。

Ē中关于波莱尔集E满足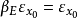的点x0称为E的α正则点，不满足上述条件的点称为E的α非正则点。

2（非）正则点常称为（非）正则点。

边界点

边界点是拓扑空间的基本概念之一。

如果点ζ的任何邻域内都既有属于集合A的点，也有不属于A的点，则称点ζ为A的一个边界点。A的所有边界点组成的集合称为A的边界。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学

维纳判别法

图文简介

维纳判别法（Wiener criterion）是波莱尔集E的边界点x0为E的α非正则点的充分必要条件。