是描述零容集与位势的关系的论断，埃文斯定理中的位势常称为埃文斯位势（Evans potential）。

简介埃文斯定理

埃文斯定理的推广形式分如下三种情形叙述：

1.若E是Rn(n≥3)的Gδ集且牛顿容量为零，则存在μ≥0，使在E上且仅在E上取+∞值并有μ(R\E)=0（从而在R\E内调和）；

2.若E是R的零容紧集，则有相应的对数位势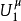满足1中条件；

3.若在R(n≥2)考虑α容量为零的Gδ集E，仍存在仅在E上取+∞值的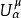，但μ(R\E)=0未必成立，当E为紧集时则成立。

定义

埃文斯定理中的位势常称为埃文斯位势。1

位势

一般位势是经典位势的一种直接推广形式，常为一个二元数值函数（核）关于某个测度的积分。

设(Ω,𝓕)是一个可测空间，K(x,y)是从Ω×Ω到[-∞,+∞]的可测函数，μ是𝓕上的实测度。若对每个x∈Ω，下式中的积分有意义，则由Ω到[-∞,+∞]的函数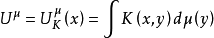称为μ以K为核的一般位势，简称位势。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

埃文斯位势

图文简介

是描述零容集与位势的关系的论断，埃文斯定理中的位势常称为埃文斯位势（Evans potential）。