Wigner-Seitz胞以Eugene Wigner和Frederick Seitz命名，是用于固态物理中晶体材料研究的一种Voronoi电池。

晶体的独特性质是它的原子排列成规则的三维阵列，称为晶格。 归因于晶体材料的所有特性都源于这种高度有序的结构。 这种结构表现出离散的平移对称性。 为了模拟和研究这种周期系统，需要一个数学“手柄”来描述对称性，并由此得出关于这种对称性所导致的材料性质的结论。 Wigner-Seitz胞是实现这一目标的一种手段。

Wigner-Seitz胞是一个原始单元的例子，它是一个单元格，它恰好包含一个格点。 空间中的点的轨迹更接近该格点而不是任何其他格点。

像任何原始细胞一样，Wigner-Seitz胞是晶格离散平移对称性的基本区域。 动量空间中倒易晶格的原始单元称为布里渊区。

定义

围绕格点的Wigner-Seitz胞被定义为空间中更接近该格点的点的轨迹比任何其他格点的轨迹。

从数学上可以看出，Wigner-Seitz胞是跨越整个直接空间的原始细胞，没有留下任何空隙或空洞。

互惠空间中的Wigner-Seitz胞被称为第一个布里渊区。 它是通过绘制与连接最近格点到特定格点的线段垂直的平面，通过这些段的中点1。

构建胞

胞可以通过首先挑选格点来选择。 选择一个点后，会将线绘制到所有附近（最近的）格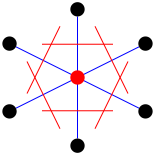点上。 在每条线的中点处，另一条线垂直于第一组线中的每条线绘制。

在三维网格的情况下，在网格点之间的线的中点绘制垂直平面。 通过使用这种方法，最小面积（或体积）以这种方式被包围，并被称为Wigner-Seitz原始胞。 晶格内的所有区域（或空间）都将被这种类型的原始单元填充，并且不会留下间隙。

一般数学概念

体现Wigner-Seitz胞中的通用数学概念通常被称为Voronoi单元，并且针对给定的一组点位置将平面划分到这些单元中被称为Voronoi图。 虽然维格纳 - 塞茨细胞本身在直接空间中并不是最重要的，但它在互惠空间中是非常重要的。 互惠空间中的Wigner-Seitz胞称为布里渊区，其中包含有关材料是导体，半导体还是绝缘体的信息。

本词条内容贡献者为:

韩拯 - 研究员 - 中国科学院金属研究所

Wigner-Seitz胞

图文简介

Wigner-Seitz胞以Eugene Wigner和Frederick Seitz命名，是用于固态物理中晶体材料研究的一种Voronoi电池。晶体的独特性质是它的原子排列成规则的三维阵列，称为晶格。 归因于晶体材料的所有特性都源于这种高度有序的结构。 这种结构表现出离散的平移对称性。 为了模拟和研究这种周期系统，需要一个数学“手柄”来描述对称性，并由此得出关于这种对称性所导致的材料性质的结论。 Wigner-Seitz胞是实现这一目标的一种手段。Wigner-Seitz胞是一个原始单元的例子，它是一个单元格，它恰好包含一个格点。 空间中的点的轨迹更接近该格点而不是任何其他格点。像任何原始细胞一样，Wigner-Seitz胞是晶格离散平移对称性的基本区域。 动量空间中倒易晶格的原始单元称为布里渊区。