齐型空间（spaces of homogeneous type）是一种拟距离空间，是Rn的一种推广。

简介概述

齐型空间是一种拟距离空间，是Rn的一种推广。

具体内容

设ρ是集合X上的一个拟距离。即ρ是X×X→[0,+∞]的一个二元函数，满足:

1、ρ(x,y)=0当且仅当x=y；

2、对∀x,y∈X，ρ(x,y)=ρ(y,x)；

3、存在数k，使对∀x,y,z∈X，有 ，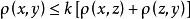

那么由P可定义一个拓扑，中心在x，半径为r>0的球B(x,r)={y∈X|ρ(x,y)0，有μ(B(x,r))0，有μ(B(x,r))≤Aμ(B(x,r))。带有上述拟距离N和正测度产的集合X，称为齐型空间(X,p,μ)。1

距离空间

设X是非空集合，对于X中任意的两个元素x与y，按某一法则都对应唯一的实数d(x,y)，而且满足下述三条公理：

(1)(非负性)d(x,y)≥0[d(x,y)=0，当且仅当x=y]；

(2)(对称性)d(x,y)=d(y,x)；

(3)(三角不等式)对于任意的x，y，z∈X，恒有d(x,y)≤d(x,z)+d(z,y)。

则称d(x,y)为x与y的距离，并称X是以d为距离的距离空间，记作(X,d)。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

齐型空间

图文简介

齐型空间（spaces of homogeneous type）是一种拟距离空间，是Rn的一种推广。