第一类切比雪夫多项式(Chebyshev polynomi-al of the first class)基本的正交多项式之一。

简介

第一类切比雪夫多项式是基本的正交多项式之一。

第一类切比雪夫方程（n为非负整数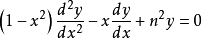） 的多项式解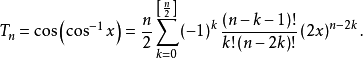， 其母函数展开式为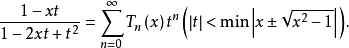

{Tn(x)}在[-1,1]上关于权函数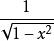 正交：

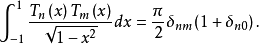
设pn(x)为在[-1,1]上xn的n-1次最佳逼近多项式，则xn-pn(x)=2-n+1Tn(x)。1

正交多项式

正交多项式是由多项式构成的正交函数系的通称。

正交多项式最简单的例子是勒让德多项式，此外还有雅可比多项式、切比雪夫多项式、拉盖尔多项式、埃尔米特多项式等，它们在微分方程、函数逼近等研究中都是极有用的工具。

切比雪夫方程

（Chebysheve quation）

切比雪夫方程是指二阶线性常微分方程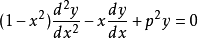 其中p为一实常数。该方程是以俄罗斯数学家巴夫尼提·切比雪夫的名字命名的。

方程的解为幂级数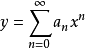 ，其中系数可通过以下递推关系式计算：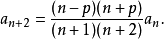

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

第一类切比雪夫多项式

图文简介

第一类切比雪夫多项式(Chebyshev polynomi-al of the first class)基本的正交多项式之一。