若测度μ是σ有限的,则称相应的测度代数为σ有限的测度代数,又称为σ有限测度环。
简介测度代数测度代数是定义了正测度的σ代数。若𝓕既是代数又是测度环,则称𝓕是一个测度代数。
设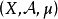 为概率空间,在
为概率空间,在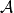 上引入等价关系:
上引入等价关系: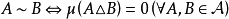 ,令
,令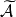 ={
={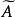 |
|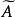 为
为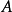 的等价类,
的等价类,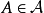 },将
},将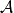 中的并、交、差、补、对称差、包含关系自然延拓到
中的并、交、差、补、对称差、包含关系自然延拓到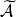 上,并定义
上,并定义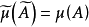 ,此时称
,此时称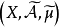 为
为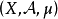 的测度代数。
的测度代数。
若测度μ是σ有限的,则称相应的测度代数为σ有限的测度代数,又称为σ有限测度环。1
测度数学上,测度(Measure)是一个函数,它对一个给定集合的某些子集指定一个数,这个数可以比作大小、体积、概率等等。传统的积分是在区间上进行的,后来人们希望把积分推广到任意的集合上,就发展出测度的概念,它在数学分析和概率论有重要的地位。
σ有限测度σ-有限测度是测度论中的一个概念。给定一个σ-代数,以及其上的一个测度μ,如果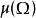 是一个有限的实数(而不是无穷大),那么就称这个测度为有限测度。如果
是一个有限的实数(而不是无穷大),那么就称这个测度为有限测度。如果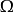 能够表示为A之中的可数多个有限测度的子集的并集,
能够表示为A之中的可数多个有限测度的子集的并集,
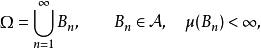 那么就称这个测度为σ-有限测度。如果的某个子集能够表示为A之中的可数多个有限测度的子集的并集,那么也称这个子集拥有σ-有限的测度。
那么就称这个测度为σ-有限测度。如果的某个子集能够表示为A之中的可数多个有限测度的子集的并集,那么也称这个子集拥有σ-有限的测度。
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学

 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助