设(Ω,𝓕)及(Ω2,𝓕2)是两个可测空间，由C作为空间Ω1×Ω2上的集类所生成的σ代数σ(C)称为𝓕1与𝓕2的乘积σ代数。

简介

设(Ω,𝓕)及(Ω2,𝓕2)是两个可测空间，令

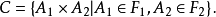由C作为空间Ω1×Ω2上的集类所生成的σ代数σ(C)称为𝓕1与𝓕2的乘积σ代数，以𝓕1×𝓕2表示，而称(Ω1×Ω2,𝓕1×𝓕2)为(Ω1,𝓕1)与(Ω2,𝓕2)的乘积空间。1

推论

C中的元素称为可测矩形，σ(C)=(𝓕1×𝓕2)中的元素称为乘积空间中的可测集。

例如，若Ω1和Ω2都是直线(-∞,+∞)，𝓕1和𝓕2都是直线上的波莱尔集的全体，则𝓕1×𝓕2正是平面上的波莱尔集的全体。然而，当𝓕1和𝓕2都是直线上的勒贝格可测集时，𝓕1×𝓕2包含在平面上的勒贝格可测集类中，但确有平面上的勒贝格可测集不在𝓕1×𝓕2中。

σ代数

在数学中，某个集合X上的σ代数（σ-algebra）又叫σ域（σ-field），是X的所有子集的集合（也就是幂集）的一个子集。这个子集满足对于可数个集合的并集运算和补集运算的封闭性（因此对于交集运算也是封闭的）。σ代数可以用来严格地定义所谓的“可测集”，是测度论的基础概念之一。

需要注意的是，虽然σ代数也称做σ域，但是它是布尔代数。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学

乘积σ代数

图文简介

设(Ω,?)及(Ω2,?2)是两个可测空间，由C作为空间Ω1×Ω2上的集类所生成的σ代数σ(C)称为?1与?2的乘积σ代数。