变分被积函数（variational integrand function）是变分法中研究的主要函数，又称为拉格朗日函数。

简介

变分被积函数是变分法中研究的主要函数。

形如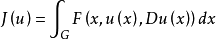的泛函J(u)称为变分积分，函数F(x,z,p)称为变分被积函数或拉格朗日函数。

推广

Ω是Rn中的区域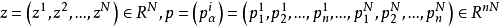，表示函数u对各自变量的偏导数，这里u也可以是向量值函数。

当u是一元数量函数时，则用y表示，J(u)记为J(y)，并称为最简变分积分。1

变分法

变分法是17世纪末发展起来的一门数学分支，是处理函数的数学领域，和处理数的函数的普通微积分相对。它最终寻求的是极值函数：它们使得泛函取得极大或极小值。变分法起源于一些具体的物理学问题，最终由数学家研究解决。

有些曲线上的经典问题采用这种形式表达：一个例子是最速降线，在重力作用下一个粒子沿着该路径可以在最短时间从点A到达不直接在它底下的一点B。在所有从A到B的曲线中必须极小化代表下降时间的表达式。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

变分被积函数

图文简介

变分被积函数（variational integrand function）是变分法中研究的主要函数，又称为拉格朗日函数。