仿积是将乘积uv化为线性部分与光滑性更高的函数之和的一种算子。若Tuv及Tvu称为仿积，而Tu及Tv称为仿积算子。

简介仿积

仿积是将乘积uv化为线性部分与光滑性更高的函数之和的一种算子。

仿积概念由科伊夫曼(Coifman,R.R.)与迈耶(Meyer,W.)引进。邦尼(Bony,J.M.)则用来处理非线性微分方程问题。

定义

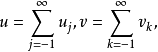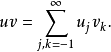设u,v∈Hs或Cρ，它们有李特尔伍德-佩利二进分解：于是按j，k的相对位置改写此和式如下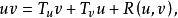：其中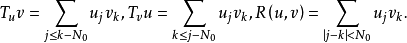选N0适当大，使得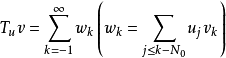也是一个李特尔伍德-佩利二进分解，并且可以证明，只要u∈L∞，则线性算子Tu:v→Tuv有Cρ→Cρ，Hs→Hs，且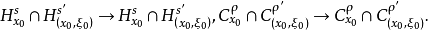

由对称性，线性算子Tv有同样性质。而当α+β>0(s+t>n/2)时，R:(u,v)→R(u,v)有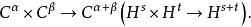

这样一来，乘积uv可用Tuv+Tvu代替，而误差项R(u,v)是光滑性更高的函数。如此得到的Tuv及Tvu称为仿积，而Tu及Tv称为仿积算子。1

算子

算子是一个函数空间到函数空间上的映射O：X→X。广义上的算子可以推广到任何空间，如内积空间等。

广义的讲，对任何函数进行某一项操作都可以认为是一个算子，甚至包括求幂次，开方都可以认为是一个算子，只是有的算子用了一个符号来代替所要进行的运算，和f(x)的f没区别，甚至和加减乘除的基本运算符号都没有区别，只是可以对单对象操作（有的符号比如大于、小于号要对多对象操作）。

又比如取概率P{X

仿积算子

图文简介

仿积是将乘积uv化为线性部分与光滑性更高的函数之和的一种算子。若Tuv及Tvu称为仿积，而Tu及Tv称为仿积算子。