涅梅茨基算子是在非线性微分方程和非线性积分方程的研究中起重要作用的一类非线性算子。这一类算子，是涅梅茨基在1934年首先提出并加以研究的。

简介

涅梅茨基算子是在非线性微分方程和非线性积分方程的研究中起重要作用的一类非线性算子。这一类算子，是涅梅茨基在1934年首先提出并加以研究的。

设G是RN中的可测集，m(G)≠0，若f(x,u)满足卡拉西奥多里条件，则算子fφ=f(x,φ(x))称为涅梅茨基算子。

性质

涅梅茨基算子将可测函数映为可测函数。

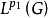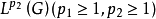涅梅茨基算子的一个重要性质是：如果fφ=f(x,φ(x))映入，则f是连续算子，并且是有界算子。

而f映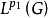入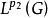的充分必要条件是存在常数b>0及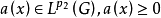，使得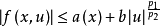对任给x∈G，u∈R1成立。1

非线性算子

非线性算子又称非线性映射，是不满足线性条件的算子。

泛函分析的研究对象主要是线性算子及其特殊情况线性泛函。但是，自然界和工程技术中出现的大量问题都是非线性的。数学物理中的一些线性方程其实都是在一定条件下的近似。为研究这些非线性问题，涉及到的算子（映射）将不能只局限于线性算子。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学

涅梅茨基算子

图文简介

涅梅茨基算子是在非线性微分方程和非线性积分方程的研究中起重要作用的一类非线性算子。这一类算子，是涅梅茨基在1934年首先提出并加以研究的。