道格拉斯泛函是道格拉斯(Douglas,J.)为解决极小曲面问题引进的一个泛函。

简介

道格拉斯泛函是道格拉斯(Douglas,J.)为解决极小曲面问题引进的一个泛函。1

其表达式为

极小曲面问题

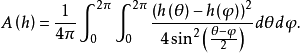
极小曲面是一种特殊曲面。张在给定的空间闭曲线Γ上有最小面积的曲面称为极小曲面。

在非参数情形下，求极小曲面的问题可以化为求曲面面积泛函

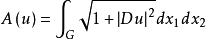的极小值，其中Ω是曲面在x1x2平面上的投影，u是曲面上的点到x1x2平面的距离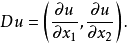，由相应的欧拉-拉格朗日方程可以推出极小曲面的平均曲率处处为零。

泛函

泛函是数学中重要的基本概念，是现代数学的重要研究对象之一，也是数学与其它领域研究与应用的一个重要工具。泛函分析是研究拓扑线性空间到拓扑线性空间之间满足各种拓扑和代数条件的映射的分支学科。

泛函是20世纪30年代形成的。从变分法、微分方程、积分方程、函数论以及量子物理等的研究中发展起来的，它运用几何学、代数学的观点和方法研究分析学的课题，可看作无限维的分析学。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所

道格拉斯泛函

图文简介

道格拉斯泛函是道格拉斯(Douglas,J.)为解决极小曲面问题引进的一个泛函。