复子流形是复流形的子流形。n维复流形M的一个开连通子集是M的n维复子流形。

简介

复子流形是复流形的子流形。

设M是一个m维复流形，其图册为A，N是M的一个连通子集。若对于每个x∈N，存在(U,𝜙)∈A，使得𝜙同胚地映U∩N到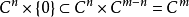的一个开子集上，则称N是M的n维复子流形。

实例

n维复流形M的一个开连通子集是M的n维复子流形。1

复流形

在数学中，特别是在微分几何和代数几何中，复流形是具有复结构的微分流形，即它能被一族坐标邻域所覆盖，其中每个坐标邻域能与n维复线性空间中的一个开集同胚，从而使坐标区域中的点具有复坐标 (z1,…,zn)，而对两个坐标邻域的重叠部分中的点，其对应的两套复坐标之间的坐标变换是全纯的。称n为此复流形的复维数。

一个n维复流形也是2n维的（实）微分流形。

子流形

子流形是单浸入映射对应的流形间的关系。

设M与N是两个微分流形，φ:M→N是C∞映射，若φ是单射，且φ是浸入，则称(M,φ)是N的子流形。或等价地定义为：M作为点集是N的子集，且从M到N的恒等映射是M到N中的嵌入，就称M为N的子流形。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学

复子流形

图文简介

复子流形是复流形的子流形。n维复流形M的一个开连通子集是M的n维复子流形。