复环面是实环面的推广。若复环面可嵌入复射影空间中作为非奇异子流形，则称这个复环面为阿贝尔流形。

简介

复环面是实环面的推广。

将复矢量空间Cm看做实2m维矢量空间R2m。在R2m中取2m个实线性无关的矢量{Vα}，它产生如下的格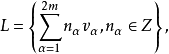：这里Z表示整数群。Cm和L都是加群，商空间Cm/L成为一个m维的复流形，称为m维复环面。1

性质

若复环面可嵌入复射影空间中作为非奇异子流形，则称这个复环面为阿贝尔流形。

阿贝尔(Abel,N.H.)流形是代数几何和数论的一个重要对象。

环面

（torus）

环面是一个面包圈形状的旋转曲面，由一个圆绕一个和该圆共面的一个轴回转所生成。在拓扑学上，环面是一个定义为两个圆的积的闭合曲面。

在几何上，一个环面是一个面包圈形状的旋转曲面，由一个圆绕一个和该圆共面的一个轴回转所生成。球可以视为环面的特殊情况，也就是旋转轴是该圆的直径时。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学

复环面

图文简介

复环面是实环面的推广。若复环面可嵌入复射影空间中作为非奇异子流形，则称这个复环面为阿贝尔流形。