模E子流形（submanifold of module E）是模E的Ck流形满足某些条件的子集。

简介

模E子流形是模E的Ck流形满足某些条件的子集。

设Y是模E的Ck流形X的一个子集，若存在E的一个闭子空间F和X的一个图册{(Ui,𝜙i)}，使当Ui∩Y≠∅时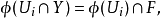，则称Y是X的子流形。

性质

不难验证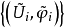是模F的子流形Y的一个Ck图册，其中Ũi=Ui∩F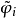，是𝜙i在Ũi上的限制。若X是一个E流形，f:X→R是可微映射，c不是f的临界点，则Y=f-1(c)就是X的一个子流形。设Y是E流形X的一个子流形，F1是E的子空间。若F1可以给出E的一个拓扑余子空间F2，则称Y为可余子流形。

推广

设X与Y分别为模E与F的两个微分流形，可微映射f:Y→X。若对每一点y∈Y，f'(y)是Ty(Y)到Tf(y)(X)的一个子空间上的一个同构，而该子空间同E中可余的固定子空间F1同构，则称f是浸入映射，或简称浸入。

设X与Y是两个巴拿赫流形，f:Y→X是一个同构，则每一点y∈Y有一个邻域V，使得f(V)是X的微分同胚于V的子流形。

一个单射的浸入就称为嵌入；一个同胚的嵌入称为正则嵌入。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学

模E子流形

图文简介

模E子流形（submanifold of module E）是模E的Ck流形满足某些条件的子集。