横截映射是像点具有某种性质的映射。若f为横截于S的映射,且P=f-1(S),则(P,i)是M的一个子流形,其中i为包含映射。
简介横截映射是像点具有某种性质的映射。
设f:M→N是m维微分流形M与n维微分流形N之间的可微映射,S是N的p维子流形,若对于x∈M,有f(x)∉S或者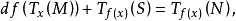 则称f在点x处横截于子流形S;若J在M的每点处横截于S,则称f横截于S,其中的加法是直和。
则称f在点x处横截于子流形S;若J在M的每点处横截于S,则称f横截于S,其中的加法是直和。
关于横截映射的一个重要结论是:若f为横截于S的映射,且P=f-1(S),则(P,i)是M的一个子流形,其中i为包含映射。1
可微映射设D是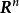 中的一个区域,
中的一个区域,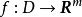 是以D为定义域的映射,
是以D为定义域的映射,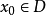 ,如果对于自变量
,如果对于自变量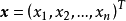 的增量
的增量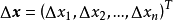 ,因变量
,因变量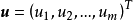 的增量
的增量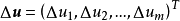 可以分解为
可以分解为
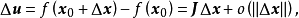 其中
其中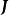 是一个
是一个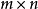 阵,
阵,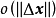 是m维空间
是m维空间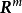 中的向量,它的各分量均是比
中的向量,它的各分量均是比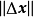 高阶的无穷小量,则称映射
高阶的无穷小量,则称映射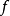 在
在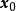 点可微,其微分为
点可微,其微分为
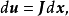 其中
其中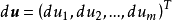 ,
,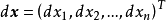 ,这里的
,这里的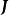 称为映射
称为映射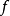 的Jacobi矩阵,也称作映射
的Jacobi矩阵,也称作映射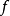 在点
在点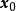 的导数,常记作
的导数,常记作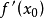 。
。
如果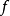 在D上的每一点处可微,则称
在D上的每一点处可微,则称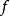 为D上的可微映射。
为D上的可微映射。
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学横截映射
图文简介
横截映射是像点具有某种性质的映射。若f为横截于S的映射,且P=f-1(S),则(P,i)是M的一个子流形,其中i为包含映射。
- 来源: 科普中国科学百科
- 上传时间:2018-11-14


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助