为使因子分析法求出因子载荷阵结构简化，便于对主因子进行专业上解释，常对因子载荷阵施行变换或称因子旋转。最常用的方法是方差最大的正交旋转法，使旋转后的因子载荷阵中的每一列元素尽可能地拉开距离，即向0或1两极分化，使每一个主因子只对应少数几个变量具有高载荷，其余载荷很小， 且每一变量也只在少数个主因子上具有高载荷，其余载荷都很小。正交旋转适用于正交因子模型，即主因子是相互独立的情况，如果主因子是彼此相关的，这时要做非正交旋转即斜交旋转1。

因子旋转(factor rotation)是一种变换，就是旋转因子的坐标轴。在因子分析中，当求得公共因子及其因子载荷阵后，对公因子要给出具有实际意义的合理解释。如果公共因子难以和实际问题相对应，可对公因子进行旋转，使得旋转后的公因子具有实际意义。常用的旋转方法有两种：方差极大的正交旋转；方差极大的斜交旋转2。

旋转的目的与方法

建立因子分析模型的目的不仅是找出主因子，更重要的是知道每个主因子的意义，以便对实际问题进行分析。如果求出主因子后，各个主因子的典型代表变量不是很突出，还需要进行因子旋转，通过适当的旋转得到比较满意的主因子3。

因子旋转的方法有很多，正交旋转(orthogonal rotation)和斜交旋转(oblique rotation)是因子旋转的两类方法。最常用的方法是最大方差正交旋转(Varimax)法。进行因子旋转，就是要使因子载荷矩阵中因子载荷的绝对值向0和1两个方向分化，使大的载倚更大，小的载荷更小。因子旋转过程中，如果因子对应轴相互正交，则称为正交旋转；如果因子对应轴相互间不是正交的，则称为斜交旋转。常见的斜交旋转方法有Promax法等。

若已经求得因子分析模型为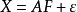，设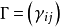为一正交矩阵，作正交变换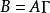，可以证明，

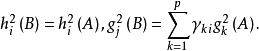
其中。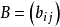

这表明经过正交旋转后，共同度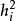并不改变，但公共因子的方差贡献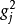不再与原来相同。这样我们就可以对因子进行合理的解释了。

对已知的因子载荷矩阵进行正交变换的目的是使各因子上的载荷两极分化，也就是要使各个因子上的载荷之间方差极大化。由于各个变量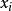在某因子上的载荷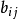的平方是该因子对该变量的共性方差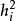的贡献，而各变量的共性方差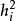一般又互不相同，若某个变量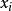的共性方差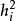较大，则分配在各个因子上的载荷就大些；反之，则小些。因此，为了消除各个变量的共性方差大小的影响，计算某因子上的载荷的方差时，可先将各个载荷的平方除以共性方差，即类似于将其标准化，然后再计算标准化后的载荷的’方差，记为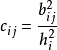。选择除以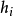是为了消除各个原始变量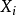对公共因子依赖程度不同的影响，而且这样的选择还不影响因子的共同度。取平方的目的是消除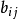符号不同的影响。

对于某一因子j，可定义其载荷之间的方差为：

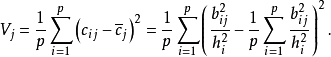
全部公共因子各自载荷之间的总方差为：

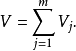
现在就是要寻找一个正交矩阵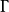，经过对已知的载荷矩阵A的正交变换后，新的因子载简矩阵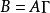中的元素能使V取得极大值3。

记因子载荷阵为

变量xi的公因子方差为

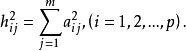称

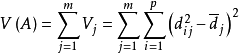为因子载荷阵A的总方差，其中

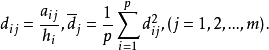
当每个因子的载荷(即A中每一列)的绝对值趋于0或1时，V(A)值就大，这时相应的公共因子具有简单的结构。所谓方差极大的正交旋转，即选择正交阵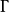，使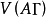达最大。当m=2时，正交阵可表为

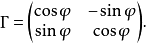适当地选择旋转角度φ，可使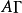的总方差达最大；当m>2时，可逐次对每两个因子进行旋转，m个公因子全部配对旋转，共需旋转次。全部旋转完结称为一轮(或一个循环，一圈)，一轮完成后再继续做下一轮，每轮后，总方差单调不减且有界，因此，该算法一定收敛，在实际计算时，当V值变化不大时，可停止旋转2。

若正交旋转后的公因子仍然没有明显的实际意义，亦可作方差极大的斜交旋转，选择适当的非退化矩阵P(P非正交阵)，使AP的总方差达最大的变换称为方差极大的斜交旋转，变换矩阵P是一般的非奇异矩阵，故具有更大的选择性。具体旋转方法与方差极大的正交旋转相同2。

本词条内容贡献者为: