罗吉斯蒂克模型（Logistic模型）是一种具有罗吉斯蒂克函数形式的非线性回归模型：Yi=β0/[1+β1exp(β2Xi)]+εi，这种函数是一种增长模型呈S形，引两条渐近线Y=0，Y=1，因此当因变量为二进制变量时，通常适用这一模型。

Logistic回归模型是分析二分类型变量时常用的非线性统计模型，是最重要且应用最广泛的非线性模型之一。该模型的因变量为二分类变量(y=0或y=1)，结果变量与自变量间是非线性关系。形式如方程(1)：

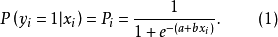
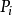指事件发生的概率，取0～11。

优点：

第一，对变量要求低，可以接受非正态分布的数据；

第二，总体预测准确率较高；

第三，数据来源直接，操作简便；

第四，判断标准明确；

第五，模型稳定，利于推广创新。

缺点：

第一，大多数时候对ST企业预测准确率较低；

第二，P值临界点的选择影响模型预测结果；

第三，违约样本与正常样本的比例影响预测结果1。

模型构造的原理简单来说是运用对数运算将事件发生与否(即事件发生概率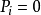或1)与自变量x间的非线性关系转化为线性关系。以单一自变量为例，具体转化步骤如下：

第一步，将上述Logistic模型方程(1)转化为如下一个非线性方程(2)。

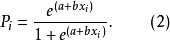
第二步，方程(2)化简转化为如下方程(3)。

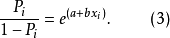
第三步，方程(3)等式两边同时取对数转化为如下方程(4)。

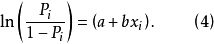
模型(4)得出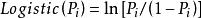与x间的线性关系方程。

此时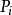，与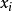虽然不存在线性关系，但是关于P的函数记作logistic(Pi)与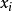存在线性关系。同理，自变量可拓展为m个，则有如下模型方程(5)。

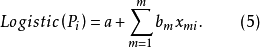
以上得到的模型同样可以用来预测事件的发生。预测时根据已知自变量与模型方程得出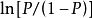，可以进一步计算事件发生的概率P。P处于0与1之间，越接近1表示发生的概率越大1。

第一，数据必须来自随机样本；

第二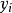，为m个自变量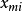的函数；

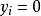第三，或1；

第四，自变量不需要呈正态分布1。

第一步，选取样本、确定初始指标；

第二步，筛选指标；

运用SPSS软件对所有指标进行Kolmogorov-Smirnov正态分布检验。符合正态分布的指标进行显著性T检验，不符合正态分布的数据进行Mann-Whitney显著性检验，去除不显著指标。进行Pearson检验，去除与其他指标存在高度相关性的指标。进行多重共线性检验，去除与其他指标存在多重共线性的指标；

第三步，进行KMO检验，确定是否进行因子分析；

第四步，进行Logistic回归，得到模型，观察模型拟合程度及预测准确率；

第五步，用检验样本检验模型预测能力；

第六步，利用模型预测事件的发生概率1。

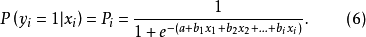
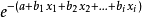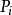当参数b大于0时，自变量x增大，减小，增大；

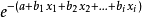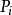当参数b小于0时，自变量x增大，增大，减小；

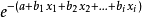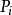当参数b等于0时，自变量x增加对无影响，不变。

因此，模型参量系数可以反映自变量x与事件发生概率P的关系。系数为正表明自变量x的增长促进事件的发生，系数为负表明自变量x的增长抑制事件的发生1。

本词条内容贡献者为: