罗吉斯蒂克变换(logistic 变换)也称罗吉脱变换,对因变量本身的指示变量、而回归函数又为罗吉斯蒂克函数时适用的一种形如Z=ln(P/(1-P))的数学变换,通过一种这种数字变换使原函数线性化,成为Z的线性函数,从而可以用最小二乘法进行回归估计。
定义罗吉斯蒂克变换(logistic 变换)也称罗吉脱变换,罗吉斯蒂克函数
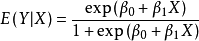 是一种非线性函数,通过一种形加
是一种非线性函数,通过一种形加
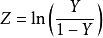 的数字变换使原函数线性化,成为Z的线性函数,从而可以用最小二乘法进行回归估计,这种变换称为罗吉斯蒂克变换1。
的数字变换使原函数线性化,成为Z的线性函数,从而可以用最小二乘法进行回归估计,这种变换称为罗吉斯蒂克变换1。
在现实问题中,人们常常要研究某一事件A发生的概率p以及p值的大小与某些因素的关系,但在许多情况下,变量x的变化,使概率在p=0或p=1的附近的变化较缓慢,很少有确定的p=0或p=1出现,于是自然的一个想法是希望寻找一个关于p的函数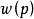 ,要求它在p=0和p=1附近变化幅度较大且
,要求它在p=0和p=1附近变化幅度较大且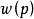 的表现形式较简单,根据这一设想研究者提出用导数
的表现形式较简单,根据这一设想研究者提出用导数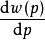 在反映
在反映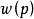 在p附近的变化,取2
在p附近的变化,取2
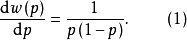 显然
显然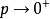 时,
时,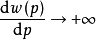 ;当
;当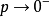 时,
时,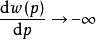 。这说明
。这说明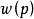 在p=0、p=1的附近变化幅度较大,用分离变量法解(1)式得到:
在p=0、p=1的附近变化幅度较大,用分离变量法解(1)式得到:
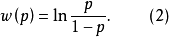 反过来看(2)式,实质上是将事件A发生的概率p与不发生的概率1一p相比(称为概率比)然后取对数。我们就称(2)式为Logistic变换。由(2)式解出:
反过来看(2)式,实质上是将事件A发生的概率p与不发生的概率1一p相比(称为概率比)然后取对数。我们就称(2)式为Logistic变换。由(2)式解出:
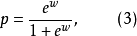 (3)式与Logistic函数(逻辑斯蒂函数)类似,该函数在研究生物的繁殖及人口估计和预测中有着广泛的应用。我们分析(3)式可以看到该函数有如下特征。
(3)式与Logistic函数(逻辑斯蒂函数)类似,该函数在研究生物的繁殖及人口估计和预测中有着广泛的应用。我们分析(3)式可以看到该函数有如下特征。
(1)无论w变化如何,其因变量p∈(0,1)当p=1和p=0时为(3)式两条水平渐近线,说明(3)的曲线图形夹在p=0和p=1两条渐近线之间。
(2)(3)式所表示的图形严格单调增函数,表明不同的y对事件发生的每个概率各不相同。同时,函数增长的特点先慢,后快,然后再趋向缓慢。大量事实表明,logistic函数的这些特征与社会生活中的许多现象较相符,它说明用logistic回归来描述事物发生的概率是可行且合理的。
如果w是某些自变量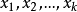 的线性函数
的线性函数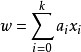 ,这时(3)式就变为下式:
,这时(3)式就变为下式:
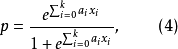
或者为:
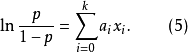
(5)式的右端保留了关于自变量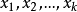 的线性性质,而左端不再是线性回归中的y,而是随机变量y,发生概率P(y=1)=p与不发生概率1-p之比的对数。我们把(5)称为广义线性logistic回归。如果(5)的右边不是
的线性性质,而左端不再是线性回归中的y,而是随机变量y,发生概率P(y=1)=p与不发生概率1-p之比的对数。我们把(5)称为广义线性logistic回归。如果(5)的右边不是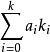 ,而是已知函数
,而是已知函数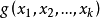 ,其中含有若干待定的参数,使下式(6)成立。
,其中含有若干待定的参数,使下式(6)成立。
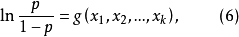 称(6)为非线性logistic回归2。
称(6)为非线性logistic回归2。
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所罗吉斯蒂克变换
图文简介
罗吉斯蒂克变换(logistic 变换)也称罗吉脱变换,对因变量本身的指示变量、而回归函数又为罗吉斯蒂克函数时适用的一种形如Z=ln(P/(1-P))的数学变换,通过一种这种数字变换使原函数线性化,成为Z的线性函数,从而可以用最小二乘法进行回归估计。
- 来源: 科普中国科学百科
- 上传时间:2018-06-19


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助