科克伦定理是科克伦于1934年提出的定理。独立正态随机变量的线性函数仍然服从正态变量,但是,独立正态随机变量的二次型函数与χ2分布有着密切的联系,科克伦定理深刻地揭示了这一问题的实质,它在方差分析问题中起着重要的作用。
基本介绍如果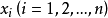 是独立的标准正态分布的变量,
是独立的标准正态分布的变量,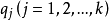 为具有秩
为具有秩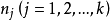 的变量
的变量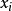 的二次式。如果
的二次式。如果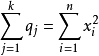 ,那么
,那么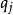 为独立的自由度分别为
为独立的自由度分别为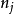 的
的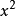 变量的充分必要条件是
变量的充分必要条件是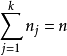 。这一定理应用到回归分析中,如果
。这一定理应用到回归分析中,如果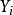 的n个观察值均来自同样的均值为
的n个观察值均来自同样的均值为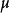 ,方差为
,方差为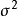 的正态分布,SSTO是总的离差平方和,自由度为n-1可分解成K个平方和SSr,其自由度分别为
的正态分布,SSTO是总的离差平方和,自由度为n-1可分解成K个平方和SSr,其自由度分别为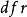 ,如果
,如果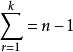 ,那么
,那么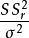 项分别是自由度为
项分别是自由度为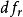 的
的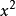 变量1。
变量1。
在线性统计推断中,科克伦(Cochran)定理及其推广形式发挥着重要的作用,它主要研究独立正态随机变量的二次型函数的性质。
科克伦定理及其证明科克伦定理 设随机变量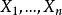 相互独立,且都服从正态分布
相互独立,且都服从正态分布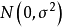 ,记
,记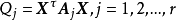 ,其中
,其中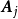 是n阶非负定的对称阵,且其秩为
是n阶非负定的对称阵,且其秩为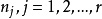 ,
,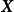 又是随机(列)向量
又是随机(列)向量
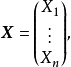
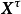 表示
表示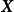 的转置
的转置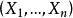 。如果
。如果
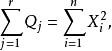 那么,
那么,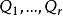 相互独立且
相互独立且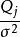 服从
服从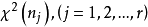 的充分必要条件是2
的充分必要条件是2
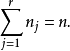 证明 不失一般性,假定
证明 不失一般性,假定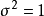 ,不然的话,可以先令
,不然的话,可以先令
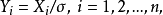 这时,
这时,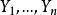 相互独立,且都服从
相互独立,且都服从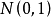 。
。
由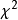 分布的可加性立即可以推得必要性成立,下面证明充分性。
分布的可加性立即可以推得必要性成立,下面证明充分性。
假定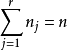 成立,对每一个
成立,对每一个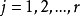 ,由于Aj是n阶非负定的方阵,因此由线性代数理论知道,存在秩为nj的
,由于Aj是n阶非负定的方阵,因此由线性代数理论知道,存在秩为nj的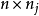 矩阵Cj,使得
矩阵Cj,使得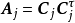 把分块矩阵
把分块矩阵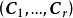 记作C。易见,C是n阶方阵。作变换
记作C。易见,C是n阶方阵。作变换
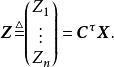 由
由
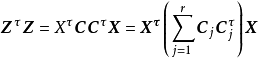
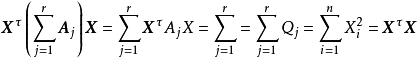
推知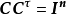 ,这里
,这里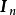 表示n阶单位阵.这表明C是正交阵。因此,
表示n阶单位阵.这表明C是正交阵。因此,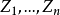 是相互独立的随机变量,且都服从N(0,1),注意到(n0理解为0)
是相互独立的随机变量,且都服从N(0,1),注意到(n0理解为0)
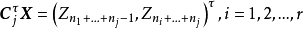
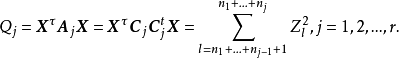 这表明
这表明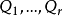 相互独立且
相互独立且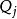 服从
服从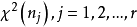 。
。
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所科克伦定理
图文简介
科克伦定理是科克伦于1934年提出的定理。独立正态随机变量的线性函数仍然服从正态变量,但是,独立正态随机变量的二次型函数与χ2分布有着密切的联系,科克伦定理深刻地揭示了这一问题的实质,它在方差分析问题中起着重要的作用。
- 来源: 科普中国科学百科
- 上传时间:2018-06-19


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助