残差是由两部分组成的，一部分是随机的，即使模型拟合得再好，它也消除不了，称为随机误差或纯误差；另一部分与模型有关，模型合适，这部分的值就小，模型不合适，这部分的值就大，称为失拟误差，对应的残差平方和由两部分构成，一部分是纯误差平方和，另一部分是拟合不佳所引起的拟合误差平方和。纯误差平方和(pure error sum of squares;SSPE或SSPE等)是模型失拟的检验中所使用的量，其自由度为∑ (ni-1)=n-c，将纯误差平方和除以自由度即为纯均方误差，通常用MSPE表示。

在重复试验的回归模型中，设自变量的取值水平共C个，共试验n次，其中每个水平F重复独立试验ni次(∑ni=n)。设因变量在第i水平下的第j次观察值为Yij，i=1，…，C，j=1，…，ni，令

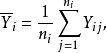表示第i水平下因变量的平均数，则

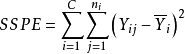称为纯误差平方和，其自由度为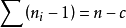，SSPE是模型失拟的检验中所使用的量。将误差平方和除以自由度即为纯均方误差，通常用MSPE表示，即1

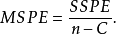
失拟检验是一种用来判断回归模型是否可以接受的检验。判断模型好坏主要通过残差分析，而残差是由两部分组成的；一部分是随机的，即使模型拟合得再好，它也消除不了，称为随机误差或纯误差；另一部分与模型有关，模型合适，这部分的值就小，模型不合适，这部分的值就大，称为失拟误差。失拟检验就是以失拟误差对纯误差的相对大小来作判断的： 倘失拟误差显著地大于纯误差，那么就放弃模型；如并不显著地大于纯误差，那么就可以接受该模型。失拟检验的前提是要求在自变量x的若干值处进行重复试验，设在xj处有nj次重复试验 (j=1，2，…，c)，记

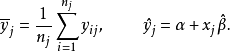则有

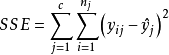
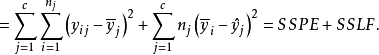其中： SSE—残差平方和，SSPE—纯误差平方和，SSLF—失拟的平方和（拟合误差平方和）。SSE，SSPE，SSLF的自由度分别为n-p-1，n-c，c-p-1。在独立、正态及等方差假定之下

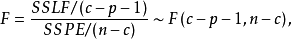对于给定置信度水平 (1-α)，如果FFα(c-p-1，n-c)，则认为失拟不显著，因而模型可以拒绝。尽管失拟检验原则上能够检验任何种类的回归模型，但通常用它来检验模型的线性假设是否合理1。

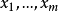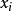设有m个试验点，在每一个处有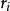次重复，其试验结果为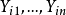，令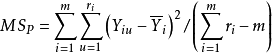 ，则MSP是 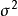的一个无偏估计。当 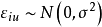相互独立时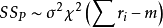， 。且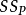 的分布不依赖于 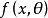的选择2。

证明 从略。

令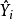表示模型在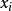点外的拟合值(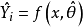)，则在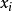点外的残差为

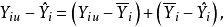从而有

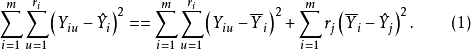即

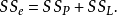其中SSE为残差平方和，SSP为纯误差平方和，SSL为拟合误差平方和。并且对应于(1)有如下的自由度分解：

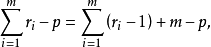其中p为模型未知参数的个数。显然，m≥p。如果m=p，则模型无拟合误差，即数据完全拟合模型。从(1)可知，模型的残差平方和由两部分构成。一部分是纯误差平方和，另一部分是拟合不佳所引起的误差平方和。

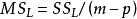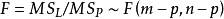令，则，这里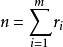。由此，可以用于检验模型拟合的好坏2。

本词条内容贡献者为: