学生化残差是残差除以它的标准差后得到的数值,用以直观地判断误差项服从正态分布这一假定是否成立 ,若假定成立,学生化残差的分布也应服从正态分布。学生化残差由普通残差推导出,在数据诊断与残差分析中应用广泛。
概念设对某量进行 次独立测量,得到的测量列
次独立测量,得到的测量列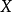 为
为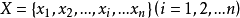 ,它的算数平方值
,它的算数平方值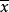 及其残差
及其残差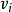 分别为:
分别为:
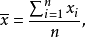
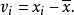 定义残差与实验标准差之比为实验学生化残差,即:
定义残差与实验标准差之比为实验学生化残差,即:
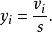 式中,
式中, 为标准差,其值为:
为标准差,其值为:
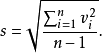
残差与样本标准差之比为样本学生化残差计算方法不变。在一般情况下,实验学生化残差和样本学生化残差均可简称为学生化残差1。
残差的绝对值与标准差之比为实验学生化残差的绝对值,即:
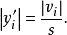 一般情况下,学生化残差的绝对值可以分为实验学生化残差的绝对值和样本学生化残差的绝对值。
一般情况下,学生化残差的绝对值可以分为实验学生化残差的绝对值和样本学生化残差的绝对值。
若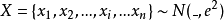 ,则
,则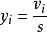 服从汤姆森
服从汤姆森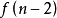 分布.
分布.
若某一测量列的样本学生化残差之绝对值的最大值为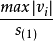 ,那么多个测量列的样本学生化残差之绝对值的最大值分别满足:
,那么多个测量列的样本学生化残差之绝对值的最大值分别满足:
当 为偶数时,
为偶数时,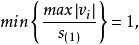
当 为奇数时,
为奇数时,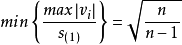 。
。
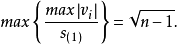
将性质2中公式两端分别乘以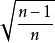 ,可得:
,可得:
当 为偶数时,
为偶数时,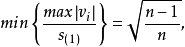
当 为奇数时,
为奇数时,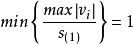 。
。
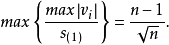
在测量上 ,残差图就是以学生化残差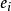 为纵坐标 ,观测值的中心化值
为纵坐标 ,观测值的中心化值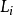 为横坐标的散点图。当有边 、角观测量时 ,可分别绘制残差图。由于残差
为横坐标的散点图。当有边 、角观测量时 ,可分别绘制残差图。由于残差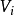 ,作为误差
,作为误差 的观测值或 “估计 应该与
的观测值或 “估计 应该与 相差不远 ,因此 ,根据残差图的大致形状是否与应有的性质相一致 ,就可以对假设的合理性提供一些有益的信息 。
相差不远 ,因此 ,根据残差图的大致形状是否与应有的性质相一致 ,就可以对假设的合理性提供一些有益的信息 。
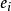
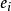
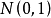 由于学生化残差
由于学生化残差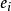 近似服从
近似服从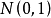 ,且近似相互独立 ,因此 ,这些可看作来自母体的简单 随机样本 。根据标准正态分布的性质 ,大约应有95%的
,且近似相互独立 ,因此 ,这些可看作来自母体的简单 随机样本 。根据标准正态分布的性质 ,大约应有95%的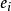 落在
落在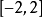 中,更进一 步约有97%的落在
中,更进一 步约有97%的落在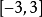 中。又因学生化残差相关性很小 ,所以,在残差图中点
中。又因学生化残差相关性很小 ,所以,在残差图中点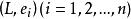 应大致落在
应大致落在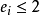 的水平带内 ,且不呈现任何趋势。
的水平带内 ,且不呈现任何趋势。
当发现残差图有异常现象 ,可对症下药 ,通过剔除异常观测值 ,或改变权阵等方法进行处理 ,直到残差图无异常现象为止 。
2.数据诊断中的应用1.强影响点
强影响点就是对统计推断有很大影响的观测数据 。到目前为止 ,已经有很多方法 度量一个观测数据对参数估计的影响 ,其中主要的一类是以 Cook 距离作为度量 影响标准的经验影响函数 。在测量上一般定义为:
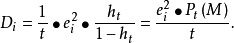 其中,
其中,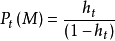 是
是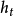 的单调递增函数。应用上常把
的单调递增函数。应用上常把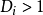 所对应的观测值称为强影响点 。强影响点对参数估值的影响类似于强权点 ,但二者又有区别 。强影响点除了同强权点一样反映了观测值在控制网结构中的位置外 ,还包含了学生化残差的影响2。
所对应的观测值称为强影响点 。强影响点对参数估值的影响类似于强权点 ,但二者又有区别 。强影响点除了同强权点一样反映了观测值在控制网结构中的位置外 ,还包含了学生化残差的影响2。
2.异常分析
一个观测值 ,如果它的学生化残差 比其它观测值的学生化残差大得多 ,就称此观测值为异常点。也就是可 能含有粗差的观测值 它有可能对平差结果产生非同小可的影响 。因此 。如何 进行粗差检测是近几年倍受重视的问题 。粗差作为模型误差 ,既可把它归入函数模型用识别法检测 ,又可把它归入随机模型用调节法处理 。
本词条内容贡献者为:
武伟 - 高级工程师 - 天津直升机有限责任公司学生化残差
图文简介
学生化残差是残差除以它的标准差后得到的数值,用以直观地判断误差项服从正态分布这一假定是否成立 ,若假定成立,学生化残差的分布也应服从正态分布。学生化残差由普通残差推导出,在数据诊断与残差分析中应用广泛。
- 来源: 科普中国科学百科
- 上传时间:2018-06-19


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助