结构式识别是从模型的结构式出发，运用“秩条件”讨论经济计量模型识别问题的一种方法。识别系指由简式推算模型结构参数可能性的讨论。若由简化式参数可以估算出结构参数，称为可识别，包括正确识别(唯一确定)和过度识别(不唯一确定)；反之，则称为不可识别。如果需要讨论结构参数的变化特性，一般的讨论顺序是：样本数据→简化式系数→“旧”的结构参数→“新”的结构参数。若由简化式系数不能估算出结构参数，那么上述研究过程便无法进行。所以，模型的识别问题是一个十分重要的问题，应该在进行任何估计以前优先考虑。“秩条件”是模型可识别的一个等价条件，即包含m个方程的线性模型中任一方程可识别等价于其他m-1个方程的变量系数至少可以找到一个非零的m-1阶行列式，而联立方程模型的每一个方程可识别定义了整个模型的可识别。应用本法的一般步骤为：(1)把模型的结构式改写成隐式函数的形式，略去随机项；(2)在系数矩阵中删去正在研究的识别方程的那行系数；(3)删去待识别方程中的非零系数的那些列；(4)试分析剩下的系数矩阵中有没有m-1阶非零行列式。如果存在，则方程是可以识别的；(5)在方程是可识别的情况下，还需根据它不包含的变量数目(其他方程包含)大于或者等于m-1来确定是过度识别或正确识别1。

如果结构方程中包含了模型中的所有变量，则该方程与模型中任何一个方程的线性组合都与该方程有相同的统计形式，因而该方程一定是不可识别的。这一事实表明，如果一个结构方程可以识别，则必然有若干个变量被排斥在该方程之外。由此可以给出判别结构方程识别性的阶条件。

模型的结构式表示为：

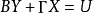或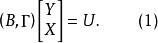

其中含有g个内生变量，k个前定变量，以及g个方程，因此它是完备的模型。假定其中第i个结构方程中所含的内生变量的个数为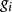，前定变量的个数为是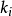，矩阵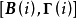为从模型系数矩阵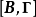中去掉第i行，并去掉第i个结构方程包含的内生变量所对应的列而形成的矩阵。对结构式模型中第i个结构方程的识别条件是2：

结构方程识别的阶条件（完备的结构型）

记M为结构模型中内生变量和前定变量的总个数（M=g+k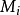），为第i个结构方程中所含变量（内生变量和前定变量）的个数：。

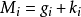当第i个结构方程是可识别时：

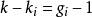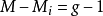若，或，称阶条件成立，此时如果第i个结构方程可识别，则第i个结构方程是恰好识别的；

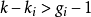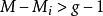若，或，称阶条件成立，此时如果第i个结构方程可识别，则第i个结构方程是过度识别的；

若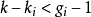，或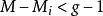，称阶条件不成立，则第i个结构方程一定不可识别。

需要指出的是，识别的阶条件只是结构方程可识别的一个必要条件，而非充要条件。即如果阶条件不成立，则对应的结构方程不可识别；如果阶条件成立，则对应的结构方程是否可识别不能确定，还需进一步通过秩条件判别2。

识别的阶条件实际上是要求某个特定方程排斥（即不包含）一定数目的变量，以保证达到其在统计形式上与模型中其他方程不同的目的。但是，它不能保证模型中的另一个方程也排斥完全相同的变量，如果这样将与待定方程具有相同的统计形式。所以，阶条件只能作为识别的必要条件。

识别的秩条件则是一个充分必要条件，其具体内容为：

在具有g个方程的结构式模型中，任何一个方程能够被识别的充分必要条件是：该方程被排斥变量结构参数矩阵的秩为g-1。或者说，该方程被排斥变量的结构参数矩阵中，至少有一个g-1阶的非零行列式。

若秩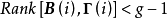，则第i个结构方程不可识别。

若秩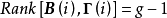，则第i个结构方程是可识别的。

其中秩条件是判断对应结构方程可否识别的充分必要条件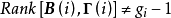，，则秩条件成立，则对应的结构方程一定可识别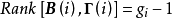；，则秩条件不成立，则对应的结构方程一定不可识别。利用秩条件可以判别结构方程是否可识别，但不能确定是恰好识别还是过度识别。

识别的秩条件实际上是要求某个特定方程所排斥的变量，必须以不同的统计形式出现在其他g-1个方程中，这样才能保证模型中的其他方程或这些方程的线性组合与待定方程具有不同的统计形式2。

设某联立方程结构式模型如下：

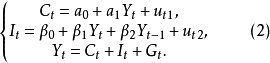
其中Y、C、I为内生变量，g=3;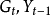和观察值始终取1的虚变量，D为预定变量，k=3。其结构式参数矩阵为：

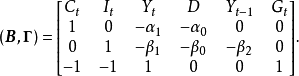对于第一个结构方程：

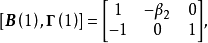
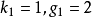，因为：

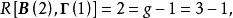所以该方程可以识别；又因为：

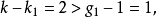所以该方程是过度识别的。

对于第二个结构方程：

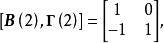
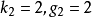，因为：

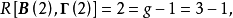所以该方程可以识别；又因为：

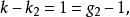所以该方程是恰好识别的。

第三个方程是平衡方程，不存在识别问题。所以该联立方程模型是可以识别的。

通过此例可以发现结构式方法要比简化式方法更简单，因而也更常用2。

本词条内容贡献者为: