如果拓扑空间X到拓扑空间Y的映射同伦于一个其值域仅含单个点的映射，则称该映射为非本质映射(inessential mapping)。不是非本质的映射称为本质映射(essential mapping)。映入一个圆周(或n维球面)而其值域不是整个圆周(或球面)的映射是非本质的。从一个区间(或n维胞腔)到一个圆周(或n维球面)中的映射是非本质的。从一个圆周到一个圆周的映射为本质的，其必要充分条件是该圆周的象关于它的中心的旋转数不等于零1。

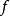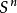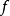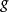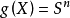设为紧空间X到m维球面 的映射，关于与同伦的任意映射 ，有 成立时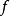， 称为本质的(essential)映射，否则称为非本质的(inessential)映射。非本质映射与“同伦于常值映射”二者是等价的2。

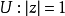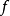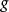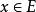定义设E是距离空间，我们称E到单位圆的连续映射是非本质的，如果存在E到R的连续映射使得对每个都有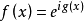。E到U的一连续映射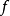称为本质的，如果它不是非本质的。（以下所有结论的证明见参考资料）3。

1. 若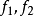都是E到U的非本质映射，则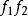与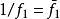也是非本质的：若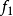是本质的而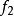是非本质的，则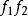与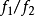都是本质的。

2. 若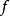是E到U的非本质映射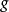，是距离空间F到E的连续映射，则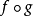是非本质的。

这些性质都是定义的直接的结果。

3. 距离空间E到U的任意连续映射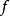，只要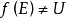，就是非本质的。

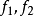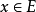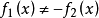4. 若是距离空间E到U的两个连续映射并使得对任意都有，又若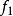是本质的(相应地，非本质的)，则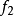也是本质的(相应地，非本质的)。

因为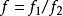，是E到U的连续映射且不取-1，于是据3它是非本质的。

5. 设E是一紧距离空间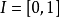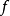，，是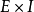到U的连续映射，若映射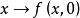是本质的(相应地，非本质的)，则映射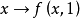也是本质的(相应地，非本质的)。

6. (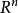中)一闭球到U的任何连续映射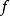都是非本质的。

7. 设A，B是距离空间E的两个闭子集，并且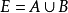与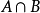是连通的，设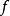是E到U的连续映射；若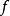到A与B上的限制都是非本质的，则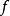也是非本质的。

8. 要U到它自身的连续映射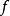为本质的，其充要条件是：对于闭路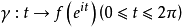有。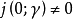

9. U到它自身的恒等映射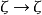是本质的3。

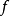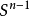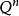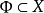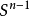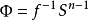维数论中主要定理之一是所谓本质映射定理(theorem on essential mappings)，它是这一理论重要部分的基础。设是从(正规)空间X到以 为边界的n维球上的连续映射，设 是在这个映射之下球面 的原象，。映射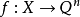称为本质的(essatial)，如果在所有点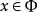上与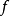一致的每个连续映射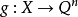都是到整个球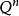上的映射。著名的Aleksandrov theorem定理说，正规空间X有维数dimX≥n，当且仅当X可被本质地映射到一个n维球上。由这个定理可以得出和定理(对于紧统，在维数论发展初期已由Menger等给出证明)：如果维数dimX=n的(正规)空间X是有限或可数多个闭子集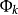的并，则这些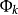中至少有一个满足。

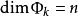关于本质映射的定理是所谓的同调维数论(homologicaldimension theory)的基础，它使我们能应用代数拓扑的方法在更为一般的假设下研究维数。空间的同调维数(homological dimension of a space)的概念与闭链和同调的概念有关，因此假定，与拓扑空间X同时还给定一个交换群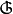，称之为系数群。于是可以谈论具有这个系数群的紧统X的闭链，它们的支撑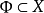，特别是谈论X中关于系数域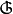同调于零的闭链4。

本词条内容贡献者为: