在抽象代数中,一个域上的代数元α之极小多项式(或最小多项式)是满足P(α)=0的最低次首一多项式(多项式内最高次项之系数为1) P。此概念对线性代数与代数扩张的研究极有助益。
简介在抽象代数中,一个域上的代数元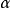 之极小多项式(或最小多项式)是满足
之极小多项式(或最小多项式)是满足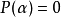 的最低次首一多项式(多项式内最高次项之系数为1)
的最低次首一多项式(多项式内最高次项之系数为1)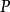 。此概念对线性代数与代数扩张的研究极有助益。1
。此概念对线性代数与代数扩张的研究极有助益。1
设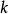 为一个域,
为一个域,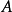 为有限维
为有限维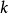 -代数。对任一元素
-代数。对任一元素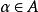 ,集合
,集合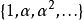 张出有限维向量空间,所以存在非平凡的线性关系 :
张出有限维向量空间,所以存在非平凡的线性关系 :
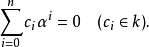
可以假设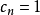 ,此时多项式
,此时多项式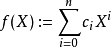 满足
满足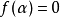 。根据多项式环里的除法,可知这类多项式中只有一个次数最小者,称之为
。根据多项式环里的除法,可知这类多项式中只有一个次数最小者,称之为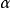 的极小多项式。
的极小多项式。
由此可导出极小多项式的次数等于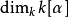 ,而且
,而且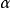 可逆当且仅当其极小多项式之常数项非零,此时
可逆当且仅当其极小多项式之常数项非零,此时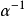 可以表成
可以表成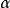 的多项式。2
的多项式。2
考虑所有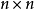 矩阵构成的
矩阵构成的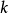 -代数
-代数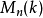 ,由于
,由于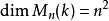 ,此时可定义一个
,此时可定义一个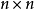 矩阵之极小多项式,而且其次数至多为
矩阵之极小多项式,而且其次数至多为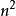 ;事实上,根据凯莱-哈密顿定理,可知其次数至多为
;事实上,根据凯莱-哈密顿定理,可知其次数至多为 ,且其根属于该矩阵的特征值集。
,且其根属于该矩阵的特征值集。
极小多项式是矩阵分类理论(若尔当标准型、有理标准形)的关键。3
极小多项式与代数扩张设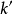 为
为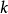 的有限扩张,此时可视
的有限扩张,此时可视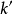 为有限维
为有限维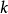 -代数。根据域的性质,极小多项式必为素多项式。元素的迹数及范数等不变量可以从极小多项式的系数读出。3
-代数。根据域的性质,极小多项式必为素多项式。元素的迹数及范数等不变量可以从极小多项式的系数读出。3
伽罗瓦扩张
本词条内容贡献者为:
尹维龙 - 副教授 - 哈尔滨工业大学极小多项式
图文简介
在抽象代数中,一个域上的代数元α之极小多项式(或最小多项式)是满足P(α)=0的最低次首一多项式(多项式内最高次项之系数为1) P。此概念对线性代数与代数扩张的研究极有助益。
- 来源: 科普中国科学百科
- 上传时间:2018-06-15


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助