秩为n的含n个未知数的n个线性方程的方程组称为克莱姆组。这样的方程组有唯一解，我们可以借助于行列式除法将它表示出来(克莱姆公式)。

克莱姆组是指秩为n的含n个未知数的n个线性方程的方程组。这样的方程组有唯一解，我们可以借助于行列式除法将它表示出来(克莱姆公式)。例如，方程组

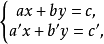当且仅当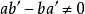 时，是克莱姆方程组，在这种情况下，克莱姆公式可写成

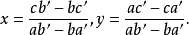
除这种情况以外，克菜姆公式虽有理论上的价值，但对数值应用来说并不好用，较为常用的有高斯主元法，或建立在矩阵分解基础上的类似方法，像在数值方程情况中那样，也可用逐次逼近法1。

把

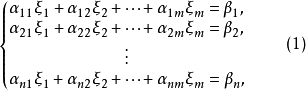叫做含m个未知元n个方程的线性方程组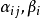， 是线性方程组中已知的元素，未知量 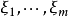是线性方程组中需要寻求的元素，满足这个方程组的任何序列( 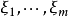)叫做一个解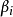， 叫做右边，若 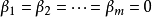，方程组叫做齐次方程组，齐次方程组至少有一个称为零解的解 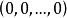。对于任意的 ，将右边用0代替后所得的新方程组叫做与原方程组相伴的齐次方程组。

定理 假定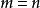 就是说方程个数和未知量个数一样多时，下列条件便彼此成立：

（i）矩阵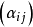 可逆；

（ii）不论右边为何，方程组（1）至少有一解；

（iii）不论右边为何，方程组（1）至多有一解；

（iv）不论右边为何，方程组（1）有而且只有一解；

（v） ；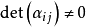

（vi）相伴齐次方程组只有零解。

定义 若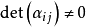 ，方程组（1）便叫做克莱姆组2。

让我们首先来考察含两个变量两个线性方程的方程组，它的一般形式为

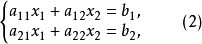用代数加法求解它。为此将第1个方程乘以 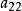，将第2个方程乘以 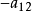，然后将它们相加；再将第1个方程乘以 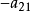，第2个方程乘以 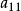，同样将它们相加。如果 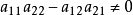，则得公式

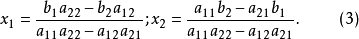
式(3)中的分母是相同的，且不难看出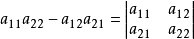， ，即它是方程组(2)的系数行列式。

式(3)中的分子同样可表示为行列式

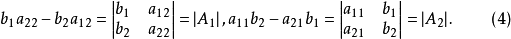容易看出，行列式 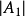是以自由项替换行列式 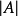中变量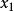 的系数而得到的，行列式 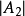是以自由项替换行列式 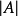中变量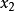 的系数而得到的，因此式(3)可写成

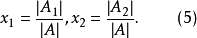
因而，如果方程组(2)的行列式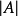异于零，则方程组是相容的，而它的解可由式(5)求出，式(5)称为克莱姆公式。

定理 如果含有n个变量n个线性方程的方程组的系数行列式不等于零，则这个方程组是确定的，它的唯一解可按下列公式求出： ·

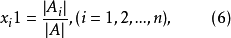式中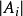 是在方程组的系数行列式 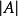中以自由项替换变量 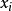的系数而得到的行列式3。

本词条内容贡献者为: