皮尔森卡方检验(英语:Pearson's chi-squared test)是最有名卡方检验之一(其他常用的卡方检验还有叶氏连续性校正、似然比检验、一元混成检验等等,它们的统计值之机率分配都近似于卡方分配,故称卡方检验)。“皮尔森卡方检验”最早由卡尔·皮尔森在1900年发表,用于类别变数的检验。科学文献中,当提及卡方检验而没有特别指明类型时,通常即指皮尔森卡方检验。1
原假设“皮尔森卡方检验”的虚无假设(H0)是:一个样本中已发生事件的次数分配会遵守某个特定的理论分配。
在虚无假设的句子中,“事件”必须互斥,并且所有事件总机率等于1。或者说,每个事件是类别变量(英语:categorical variable)的一种类别或级别。
简单的例子:常见的六面骰子,事件=丢骰子的结果(可能是1~6任一个)属于类别变量,每一面都是此变量的一种(一个级别)结果,每种结果互斥(1不是2, 3, 4, 5, 6; 2不是1, 3, 4 ...),六面的机率总和等于1。
用途和步骤“皮尔森卡方检验”可用于两种情境的变项比较:适配度检验,和独立性检验。1
“适配度检验”验证一组观察值的次数分配是否异于理论上的分配。
“独立性检验”验证从两个变量抽出的配对观察值组是否互相独立(例如:每次都从A国和B国各抽一个人,看他们的反应是否与国籍无关)。
不管哪个检验都包含三个步骤:
(1)计算卡方检验的统计值“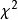 ”:把每一个观察值和理论值的差做平方后、除以理论值、再加总。
”:把每一个观察值和理论值的差做平方后、除以理论值、再加总。
(2)计算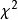 统计值的自由度“df”。
统计值的自由度“df”。
(3)依据研究者设定的置信水准,查出自由度为df的卡方分配临界值,比较它与第1步骤得出的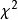 统计值,推论能否拒绝虚无假设。
统计值,推论能否拒绝虚无假设。
适配度检验(英语:Goodness of Fit test):测试样本的机率分配与母体有多相似。
母体假设为离散型均匀分配
当理论上的母体分配为每个类别机率一致时,即应适用离散型均匀分配的计算方法。N个观察值于理论上应均匀分配在所有的 m个字段(类别)中,因此每个字段(类别)的“理论次数”(或期望次数)为:
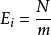 ,其中i=1,2,...,m.
,其中i=1,2,...,m.
其中,自由度df=m-1 。“m”是总共要计算离差平方的个数(每个类别计算一次观察值与理论值的差,再平方)。“ -1”是因为对于计算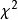 而言只有一个限制条件:观察值的个数总和为N。
而言只有一个限制条件:观察值的个数总和为N。
在同一个个体(例如:同一个人)身上有两个二元变量(X, Y),例如 X(男/女)和 Y(右撇子/左撇子),观察两个变量的相关性。虚无假设是:两个变量呈统计独立性。
在本例中:性别与惯用手是独立事件。
首先,每个观察值(每个抽出的人)会被重新编排到一个叫做“列联表”(英语:contingency table,又称:条件次数表)的二维表格里。本例的列联表是2×2的构造:
| 43 | 44 | 87 |
| 9 | 4 | 13 |
| 52 | 48 | 100 |
如果列联表共有 r 行 c 列,那么在独立事件的假设下,每个字段的“理论次数”(或期望次数)为:
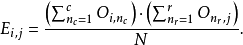
其中N是样本大小(观察值的个数,亦即2×2列联表所有字段的总和,本例:N = 100)。本例的各字段期望值如下(括号里的数字):
| 43 (45.24) | 44 (41.76) | 87 |
| 9 (6.76) | 4 (6.24) | 13 |
| 52 | 48 | 100 |
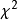 统计值的公式是:
统计值的公式是:
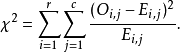 本例的
本例的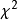 统计值是:
统计值是:
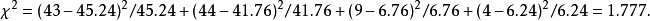 自由度df=(r-1)(c-1)是这样得出:虽然总共要计算 rc 个离差平方(每个字段计算一次观察值与理论值的差,再平方),但 X 变量有1个限制条件(样本抽出后,男性的人数即固定),Y 变量也有1个限制条件(样本抽出后,右撇子的人数即固定),所以可自由变动的字段数只有 (r-1)(c-1).
自由度df=(r-1)(c-1)是这样得出:虽然总共要计算 rc 个离差平方(每个字段计算一次观察值与理论值的差,再平方),但 X 变量有1个限制条件(样本抽出后,男性的人数即固定),Y 变量也有1个限制条件(样本抽出后,右撇子的人数即固定),所以可自由变动的字段数只有 (r-1)(c-1).
在本例中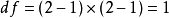 .
.
在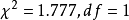 的条件下,得出卡方分配右尾机率p=0.1825,无法拒绝虚无假设,亦即:无法拒绝性别变量与惯用手变量互相独立的假设。
的条件下,得出卡方分配右尾机率p=0.1825,无法拒绝虚无假设,亦即:无法拒绝性别变量与惯用手变量互相独立的假设。
如果个别字段的期望次数太低,会使机率分配无法近似于卡方分配。一般要求:自由度df>1时,期望次数小于5的字段不多于总字段的20%。2
若自由度df=1,且若期望次数
皮尔森卡方检验
图文简介
皮尔森卡方检验(英语:Pearson's chi-squared test)是最有名卡方检验之一(其他常用的卡方检验还有叶氏连续性校正、似然比检验、一元混成检验等等,它们的统计值之机率分配都近似于卡方分配,故称卡方检验)。“皮尔森卡方检验”最早由卡尔·皮尔森在1900年发表,用于类别变数的检验。科学文献中,当提及卡方检验而没有特别指明类型时,通常即指皮尔森卡方检验。
- 来源: 科普中国科学百科
- 上传时间:2018-06-14


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助