若函数f(x)在闭区间[a,b]上连续,则它在[a,b]上一致连续。换言之,在闭区间上连续的函数在该闭区间一致连续。
历史上比较著名的康托(Cantor)定理,大致有下列三个:
康托定理1:闭区间上的连续实函数是一致连续的。1
康托定理2:一个集合本身的势严格小于其幂集的势。
康托定理3:如果一个全序集是可列集,且是稠密的,无最大和最小值的,则它一定和有理数集序同构。
定理若函数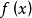 在闭区间
在闭区间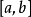 上连续,则它在
上连续,则它在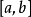 上一致连续。
上一致连续。
设函数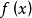 在区间
在区间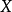 上定义,则
上定义,则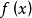 在
在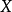 上一致连续的充分必要条件是:对任何点列
上一致连续的充分必要条件是:对任何点列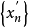
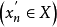 和
和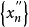
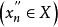 ,只要满足
,只要满足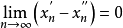 ,就成立
,就成立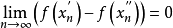 。
。
函数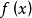 在有限开区间
在有限开区间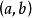 连续,则
连续,则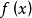 在
在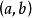 上一致连续的充分必要条件是
上一致连续的充分必要条件是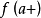 与
与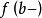 存在。
存在。
采用反证法。
假设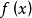 在
在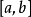 上非一致连续,由非一致连续定义可知存在
上非一致连续,由非一致连续定义可知存在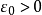 及两点列
及两点列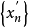 和
和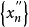 ,
,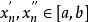 ,满足
,满足
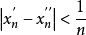 ,且
,且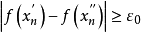
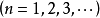 。
。
因为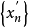 有界,由Bolzano-Weierstrass定理,存在收敛子列
有界,由Bolzano-Weierstrass定理,存在收敛子列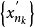 :
:
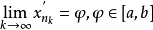
在点列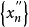 中取子列
中取子列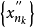 ,其下标与
,其下标与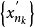 下标相同,则由
下标相同,则由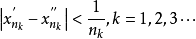 ,又得到
,又得到
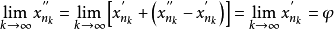
由于函数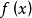 在点
在点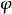 连续,因而有
连续,因而有
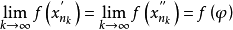
于是得到:
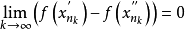
但这与假设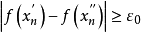 产生矛盾,从而推翻假设,得到
产生矛盾,从而推翻假设,得到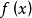 在
在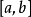 上的一致连续的结论。
上的一致连续的结论。
例: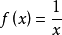 在
在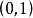 上连续,但非一致连续。
上连续,但非一致连续。
证:对于任意给定的 ,
,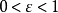 ,我们通过精确地解出
,我们通过精确地解出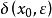 ,来说明不存在适用于整个区间
,来说明不存在适用于整个区间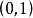 的
的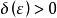 。
。
对任意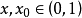 ,关系式
,关系式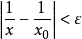 即为
即为
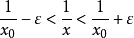 它等价于
它等价于
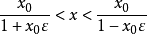 即
即
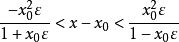 由此得到
由此得到
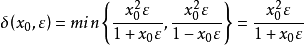 显然,这就是
显然,这就是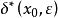 。
。
但是当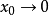 时,
时,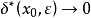 ,换言之,不存在对区间
,换言之,不存在对区间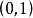 中一切点都适用的
中一切点都适用的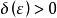 ,因此
,因此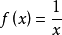 在
在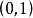 上非一致连续。1
上非一致连续。1
本词条内容贡献者为:
朱坤平 - 副教授 - 华东理工大学

 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助