R树是用来做空间数据存储的树状数据结构。例如给地理位置，矩形和多边形这类多维数据建立索引。R树是由Antonin Guttman于1984年提出的。1人们随后发现它在理论和应用方面都非常实用。 在现实生活中，R树可以用来存储地图上的空间信息，例如餐馆地址，或者地图上用来构造街道，建筑，湖泊边缘和海岸线的多边形。然后可以用它来回答“查找距离我2千米以内的博物馆”，“检索距离我2千米以内的所有路段”（然后显示在导航系统中）或者“查找（直线距离）最近的加油站”这类问题。R树还可以用来加速使用包括大圆距离在内的各种距离度量方式的最邻近搜索。

近二十多年来，许多学者致力于R树的研究，在R树的基础上衍生出了许多变种。比较典型的有R+树、R*树、压缩R树等。

1.除根结点之外，所有非根结点包含有m至M个记录索引（条目）。根结点的记录个数可以少于m。通常，m=M/2。

2.对于所有叶子中存储的记录（条目），I是最小的可以在空间中完全覆盖这些记录所代表的点的矩形（注意：此处所说的“矩形”是可以扩展到高维空间的）。

3.对于所有非叶子结点上的记录（条目），i是最小的可以在空间上完全覆盖这些条目所代表的点的矩形（同性质2）。

4.所有叶子结点都位于同一层，因此R树为平衡树。

R*树

R+树

Hilbert R树

X树

R树的核心思想是聚合距离相近的节点并在树结构的上一层将其表示为这些节点的最小外接矩形，这个最小外接矩形就成为上一层的一个节点。2R树的“R”代表“Rectangle（矩形）”。因为所有节点都在它们的最小外接矩形中，所以跟某个矩形不相交的查询就一定跟这个矩形中的所有节点都不相交。叶子节点上的每个矩形都代表一个对象，节点都是对象的聚合，并且越往上层聚合的对象就越多。也可以把每一层看做是对数据集的近似，叶子节点层是最细粒度的近似，与数据集相似度100%，越往上层越粗糙。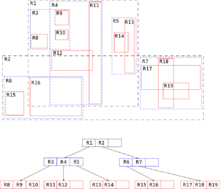

跟B树类似，R树也是平衡树（所以所有叶子节点都在同一深度）。它把数据按（内存）页存储，是为磁盘存储设计的（跟数据库的做法相同）。每一页可以存储不超过一个上限的条目，这个上限一般用{\displaystyle M}表示。R树会在除根节点以外的节点上维持数据条目不小于最小条目数。根据经验，最小条目数在条目上限的30%–40%时性能最佳，而B树会维持条目上限的50%，B*树甚至维持条目上限的66%。这么做的原因是平衡空间数据比平衡B树上的线性数据更复杂。

跟其他树结构一样，R树的搜索算法（例如：交集，子集，最邻近搜索）也非常简单。核心思想是画出查询语句相应的边框，并用它来决定要不要搜索某个子树。这样在搜索时可以跳过树上的大部分节点。跟B树类似，这个特性让R树可以把整棵树放在磁盘里，在需要的时候再把节点读进内存页，从而可以应用在大数据集和数据库上。

R树的主要难点在于构建一棵既能保持平衡（所有叶子节点在同一层），又能让树上的矩形既不包括太多空白区域也不过多相交（这样在搜索的时候可以处理尽量少的子树）的高效的树。例如，最初的通过插入节点来构建一棵高效的R树的构想是选择一棵子树插入，使得对其外接矩形的扩张最小。填满一页后，把数据分成两份，使它们分别包括尽量小的区域。大部分关于R树的研究和改进都是关于如何改进建树的过程。它们可以分为两类，一类是如何从头开始构建一棵高效的树（被称为批量加载），另一类是如何在一棵已经存在的树上插入和删除。

R树不保证最坏情况下的性能，但是在现实数据上一般表现不错。理论上来说，批量加载的优先级R树是最坏情况下的最优解，但由于复杂度太高，还没有在实际应用中获得关注。

当数据被构建成R树时，任意Lp空间中的数据的最近k个邻居都可以很高效地用空间交集计算。这对很多基于最近邻居法的算法（例如本地异常因子算法）都很有帮助。DeLi-Clu提出的Density-Link-Clustering是一种使用R树来进行空间交集，从而高效地计算OPTICS聚类的聚类分析算法.

R树是一个高度平衡树，它是B树在k维上的自然扩展，用空间对象的MBR来近似表达空间对象，根据地物的MBR建立R树，可以直接对空间中占据一定范围的空间对象进行索引。3R树的每一个结点都对应着磁盘页D和区域I，如果结点不是叶结点，则该结点的所有子结点的区域都在区域I的范围之内，而且存储在磁盘页D中。如果结点是叶结点，那么磁盘页D中存储的将是区域I范围内的一系列子区域，子区域紧紧围绕空间对象，一般为空间对象的外接矩形。

R树中每个结点所能拥有的子结点数目是有上下限的。下限保证索引对磁盘空间的有效利用，子结点的数目小于下限的结点将被删除，该结点的子结点将被分配到其他的结点中；设立上限是因为每一个结点只对应一个磁盘页，如果某个结点要求的空间大于一个磁盘页，那么该结点就要被划分为两个新的结点，原来结点的所有子结点将被分配到这两个新的结点中。令M为一个结点中记录数目的最大值，mSM/2为一参数，说明一个节点记录的最小值，m可作为调节树结构的一个可变参数，R树满足如下几项特点：

1．根节点若非叶子节点，则至少有两个子节点；

2．每个非根叶节点和非叶节点包含的实体个数均介于m和M之间；

3．所有叶子节点在同一层次；

R树兄弟结点对应的空间区域可以重叠，可以较容易地进行插入和删除操作。但正因为区域之间有重叠，空间索引可能要对多条路径进行搜索后才能得到最后的结果。当查找与给定的查询窗口相交的所有空间对象时，空间搜索算法是从根结点开始，向下搜索相应的子树．算法递归遍历所有约束矩形与查询窗口相交的子树，当到达叶结点时，边界矩形中的元素被取出并测试其是否与查询矩形相交，所有与查询窗口相交的叶结点即为要查找的空间对象。R树的查询效率会因重叠区域的增大而大大减弱，在最坏情况下，其时间复杂度甚至会由对数搜索退化成线性搜索。正是这个原因促使了R+树的产生。

在R+树中，兄弟结点对应的空间区域没有重叠，而没有重叠的区域划分可以使空间索引搜索的速度大大提高，克服了R树中多路查询的问题，但同时它也存在着一些缺陷，如对某个最小约束矩形的划分，可能会引起相关子树上其他结点也需要重新划分，向下分裂操作可能使得已经划分好了的结点被重新划分，空间对象在R+树的叶结点中被重复标记，完成删除运算后，必须对R+树进行重建等，同时由于在插入和删除空间对象时要保证兄弟结点对应的空间区域不重叠，而使插入和删除操作的效率降低。

R*树是最有效的R树变种，它能对覆盖区域、重叠面积和边界周长进行启发式地优化，并通过重新插入节点重建R．树以提高其性能，但重新插入这个过程相当繁琐，其实现过程太过漫长。压缩R树的空间数据集是预先己知的，通过预先对数据进行合理有效的组织，可以保证其具有很高的空间利用率和良好的查询效率，但由于其不能进行动态插入和删除，因而其应用受到了很大限制。

R树是B树在多维空间的扩展，是一种平衡的树结构。R树结构采用平行于数据空间轴的最小的边界矩形来近似复杂的空间对象，其主要优点是用一定数量的字节来表示一个复杂的对象。尽管这样会丢失很多的信息，但是空间物体的最小边界矩形保留了物体的最重要的几何特性，即空间物体的位置和其在整个坐标轴上的范围。

R树的数据按（内存）页存储，每一页存储多条数据，数据条数不超过一个事先定义的最大值，一般会多于最小值。非叶子节点上的每一条数据由指向子节点的标识符和该子节点的外接矩形组成。叶子节点则存储每个对象需要的数据，一般是一个外接矩形和指向数据的标识符。如果是点数据，叶子节点只需要存储这些点本身。如果是多边形数据（一般数据量很大的多边形需要额外存储），一般的做法是在叶子节点中存储多边形的最小外接矩形和指向这个多边形的数据的标识符。

R树的搜索操作很简单，跟B树上的搜索十分相似。它返回的结果是所有符合查找信息的记录条目。而输入是不仅仅是一个范围了，它更可以看成是一个空间中的矩形。也就是说，输入的是一个搜索矩形。

先给出伪代码：

Function：Search

描述：假设T为一棵R树的根结点，查找所有搜索矩形S覆盖的记录条目。

S1:[查找子树]如果T是非叶子结点，如果T所对应的矩形与S有重合，那么检查所有T中存储的条目，对于所有这些条目，使用Search操作作用在每一个条目所指向的子树的根结点上（即T结点的孩子结点）。

S2:[查找叶子结点]如果T是叶子结点，如果T所对应的矩形与S有重合，那么直接检查S所指向的所有记录条目。返回符合条件的记录。

R树的插入操作也同B树的插入操作类似。当新的数据记录需要被添加入叶子结点时，若叶子结点溢出，那么我们需要对叶子结点进行分裂操作。显然，叶子结点的插入操作会比搜索操作要复杂。插入操作需要一些辅助方法才能够完成。

来看一下伪代码：

Function：Insert

描述：将新的记录条目E插入给定的R树中。

I1：[为新记录找到合适插入的叶子结点]开始ChooseLeaf方法选择叶子结点L以放置记录E。

I2：[添加新记录至叶子结点]如果L有足够的空间来放置新的记录条目，则向L中添加E。如果没有足够的空间，则进行SplitNode方法以获得两个结点L与LL，这两个结点包含了所有原来叶子结点L中的条目与新条目E。

I3：[将变换向上传递]开始对结点L进行AdjustTree操作，如果进行了分裂操作，那么同时需要对LL进行AdjustTree操作。

I4：[对树进行增高操作]如果结点分裂，且该分裂向上传播导致了根结点的分裂，那么需要创建一个新的根结点，并且让它的两个孩子结点分别为原来那个根结点分裂后的两个结点。

Function：ChooseLeaf

描述：选择叶子结点以放置新条目E。

CL1：[Initialize]设置N为根结点。

CL2：[叶子结点的检查]如果N为叶子结点，则直接返回N。

CL3：[选择子树]如果N不是叶子结点，则遍历N中的结点，找出添加E.I时扩张最小的结点，并把该结点定义为F。如果有多个这样的结点，那么选择面积最小的结点。

CL4：[下降至叶子结点]将N设为F，从CL2开始重复操作。

Function：AdjustTree

描述：叶子结点的改变向上传递至根结点以改变各个矩阵。在传递变换的过程中可能会产生结点的分裂。

AT1：[初始化]将N设为L。

AT2：[检验是否完成]如果N为根结点，则停止操作。

AT3：[调整父结点条目的最小边界矩形]设P为N的父节点，EN为指向在父节点P中指向N的条目。调整EN.I以保证所有在N中的矩形都被恰好包围。

AT4：[向上传递结点分裂]如果N有一个刚刚被分裂产生的结点NN，则创建一个指向NN的条目ENN。如果P有空间来存放ENN，则将ENN添加到P中。如果没有，则对P进行SplitNode操作以得到P和PP。

AT5：[升高至下一级]如果N等于L且发生了分裂，则把NN置为PP。从AT2开始重复操作。

R树的删除操作与B树的删除操作会有所不同，不过同B树一样，会涉及到压缩等操作。相信读者看完以下的伪代码之后会有所体会。R树的删除同样是比较复杂的，需要用到一些辅助函数来完成整个操作。

伪代码如下：

Function：Delete

描述：将一条记录E从指定的R树中删除。

D1：[找到含有记录的叶子结点]使用FindLeaf方法找到包含有记录E的叶子结点L。如果搜索失败，则直接终止。

D2：[删除记录]将E从L中删除。

D3：[传递记录]对L使用CondenseTree操作

D4：[缩减树]当经过以上调整后，如果根结点只包含有一个孩子结点，则将这个的孩子结点设为根结点。

Function：FindLeaf

描述：根结点为T，期望找到包含有记录E的叶子结点。

FL1：[搜索子树]如果T不是叶子结点，则检查每一条T中的条目F，找出与E所对应的矩形相重合的F（不必完全覆盖）。对于所有满足条件的F，对其指向的孩子结点进行FindLeaf操作，直到寻找到E或者所有条目均以被检查过。

FL2：[搜索叶子结点以找到记录]如果T是叶子结点，那么检查每一个条目是否有E存在，如果有则返回T。

Function：CondenseTree

描述：L为包含有被删除条目的叶子结点。如果L的条目数过少（小于要求的最小值m），则必须将该叶子结点L从树中删除。经过这一删除操作，L中的剩余条目必须重新插入树中。此操作将一直重复直至到达根结点。同样，调整在此修改树的过程所经过的路径上的所有结点对应的矩形大小。

CT1：[初始化]令N为L。初始化一个用于存储被删除结点包含的条目的链表Q。

CT2：[找到父条目]如果N为根结点，那么直接跳转至CT6。否则令P为N的父结点，令EN为P结点中存储的指向N的条目。

CT3：[删除下溢结点]如果N含有条目数少于m，则从P中删除EN，并把结点N中的条目添加入链表Q中。

CT4：[调整覆盖矩形]如果N没有被删除，则调整EN.I使得其对应矩形能够恰好覆盖N中的所有条目所对应的矩形。

CT5：[向上一层结点进行操作]令N等于P，从CT2开始重复操作。

CT6：[重新插入孤立的条目]所有在Q中的结点中的条目需要被重新插入。原来属于叶子结点的条目可以使用Insert操作进行重新插入，而那些属于非叶子结点的条目必须插入删除之前所在层的结点，以确保它们所指向的子树还处于相同的层。

本词条内容贡献者为: