科普中国公众号
科普中国微博
帮助本文由公众号 “把科学带回家” 提供
给孩子最好的科学教育
在日本朝日放送的一档叫做探偵!ナイトスクープ Knight Scoop 的节目里，有一个叫做秋原俊彦的73岁老爷爷在医生的诊室里看到了一个游戏，然后深深入迷。他求医生把这个游戏送给他，然后在家花了10年时间想解开，但是做不到。不但秋原老爷子解不开，大多数观众也被难住了。 这个游戏是这样的—— 这个游戏的目标是，在不暴力拆解的情况下，让银环从绿球这里到另一边的红球这里。 你想到的方法大家都想过了，都不是解法。 银环不可能套过中间那个木头环—— 银环也不可能从木头环的中间穿过去—— 基座拆不开，绳子也绕不过去—— 实际上，难住老爷爷的这个解密游戏历史悠久，也曾经难住了一代又一代的人。但是因为它的魅力巨大，所以一直流传到现在，而且传播到了许多国家，在西方和东亚都有不同的版本。 你能解开这个绳结捆绑游戏吗？ 关键概念 所罗门封印 材料和操作 一根木条（也可以用粗一点的吸管代替） 一根绳子 两个圆环 在木条上打3个洞，然后把绳子和圆环按照上面图片里的样子组装好，就可以开始玩啦。这个版本其实和一开始介绍的那个游戏是一样的道理，解法也是类似的。 这个游戏的目标是，让右边的那个圆环和左边的圆环贴在一起。不能把木条弄断，也不能把绳子剪断。 你想到解答方法了吗？ 如果你觉得有点难，那先用下面这个简单的题目来热热身吧。 看看下面这个情况，应该怎样把插头松绑？ 其实这个插头是这样解出来的—— 再来一道类似的题，求如何给自己松绑？ 解法—— 这有没有给你一点启示呢？ 如果你还是不知道应该怎么解，在 把科学带回家 后台回复 求求你告诉我，就可以得到答案啦。 原理 在这档 Knight Scoop 节目里，后来在日本知惠之轮协会的山本徹的帮助下，这个谜题终于得到了解答。 这个解密游戏，在西方有 wedding rings，the ox yoke，loop de loop，african ball 或者 Solomon’s seal 等各种名字。 这个游戏最早可以追溯到16世纪的意大利的数学家，达·芬奇（为什么老是你？）的老友卢卡·帕西奥利（Luca Pacioli）撰写的《De Viribus Quantitatis》（数字的力量）。 这个游戏也有东亚的版本。这幅1836年的日本图画里也描绘了这个游戏，这也是我们上面介绍手工制作的版本。 这个游戏的设定是这样的，恋人 Osome 和 Hisamatsu 因为某些原因分离了，你要努力使他们重新在一起。 有很多实用主义的人会说，这些游戏有什么用？ 其实，这些游戏和拓扑学有关。历史上拓扑学游戏曾经启发了重要的数学发现。 比如，柯尼斯堡七桥问题（Konigsberg bridge）问题就启发了欧拉。欧拉在1736年写了一篇论文证明这个问题无解。欧拉的这篇论文成为图论这个数学分支的起源。 如果上面这些游戏都难不倒你，可以试一试下面这个进阶版本的拓扑游戏。你觉得在不暴力拆解的情况下，左图可能变成右图吗？ 这个拓扑游戏其实想表达的是拓扑学里的一个基础概念：咖啡杯的拓扑形态和甜甜圈是一毛一样的。 @wikipedia 好了，在拓扑学里的解法如下。 @西山豊，大阪经济大学 好的我知道又有人要问：“这有什么用？” 很多人不是想知道小昭戴着镣铐是怎么换衣服的吗？ 这就是金庸隐藏的拓扑学答案啊！你把白色的东西看成手铐，把双手合十的小昭看成是一个圈，你看在拓扑学的世界里小昭的链子根本就没有同时铐住她的双手啊。 大概就是因为小昭暗自掌握了这个拓扑学知识，所以金庸大侠才在《倚天屠龙记》后记里提到小昭是他在书中最喜爱的角色吧。
柯尼斯堡七桥问题：当时东普鲁士柯尼斯堡（今日俄罗斯加里宁格勒）市区跨普列戈利亚河两岸，河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？
@wikipedia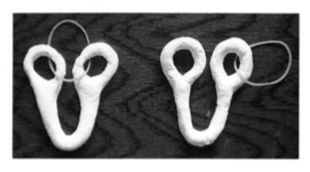
(๑• ̀д•́ )✧
京公网安备11010202008423号 京ICP备 16016202号-1