数学分岔与物理相变：不同领域的平行叙事与统一

作者：邱仲普

在物理学中，从十九世纪末居里发现铁磁体在特定温度下会突然失去磁性起，人们开始意识到自然界存在“秩序的突变”。随后外斯的平均场理论给出第一个成功的宏观描述，却忽略了临界点附近剧烈的涨落。楞次与伊辛通过自旋模型将磁性理解为有序与无序的竞争，但真正揭开相变本质的，是昂萨格在1944年对二维伊辛模型的严格求解，第一次以数学精度展示了连续相变的临界行为。杨振宁在1951年完成了自发磁化的解析推导，使理论闭环，又与李政道提出“李–杨相变定理”，将配分函数零点引入复平面，把相变转化为可解析的数学结构。随着理论的发展，相变研究从经验和近似走向严格与普适，催生了标度律、普适类与重整化群理论，成为理解复杂系统与临界现象的核心框架。

当物理学家们在物质状态的迷宫中探索时，数学家们也在绘制一幅平行的地图：他们处理的不是水或磁铁，而是方程与几何形态，却关心同样的问题——当一个系统受到外部缓慢驱动时，它的稳定性如何变化，哪些平衡点会消失，哪些新的稳定态会出现。他们以动力系统为语言，其研究核心是结构稳定性。

数学的叙事：分岔、突变与结构稳定性

想象一个在碗底静止的小球。无论你如何轻微地推它，它最终都会回到碗底。这个系统是“结构稳定”的。现在，想象你慢慢地、持续地改变碗的形状，让它从U形变为M形。在某个瞬间，碗底中央的稳定点会消失，分裂成一个不稳定的高点和两个新的稳定点。小球会突然滚向其中一个新的低谷。

这个从U到M的转变，便是数学家所说的分岔：当系统参数连续变化时，其定性行为（如平衡点的数量和稳定性）发生突变的现象。这听起来与统计物理中的相变何其相似！而数学的严谨之处在于，它为这些“突变”提供了详尽的分类。

最基础的分岔是鞍-结点分岔，在一个动力系统中（如图1A），我们会看到随着参数 r 的增大，系统的稳定平衡点和不稳定平衡点会相遇并消失，过程如图1B、C所示。

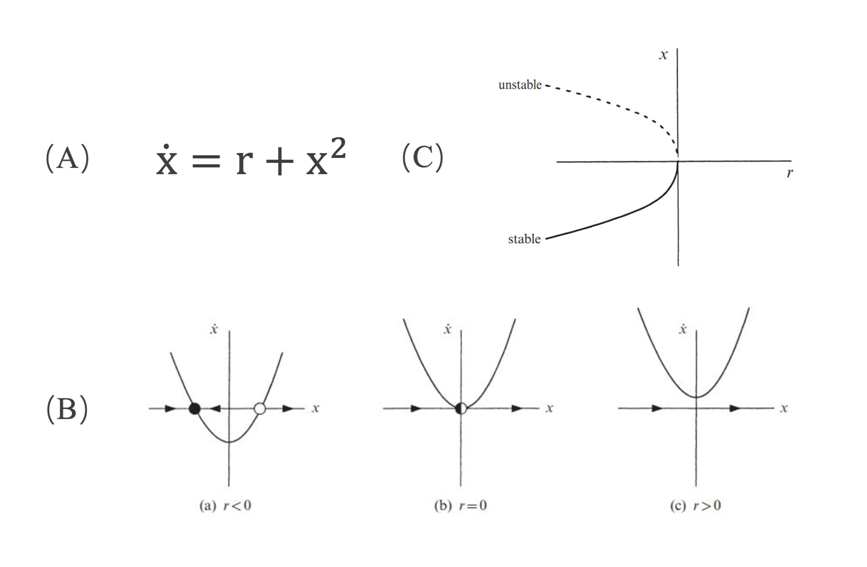
图1：鞍-结点分岔示意图，（A）动力系统的典型微分方程形式，（B）r 变化时分岔的向量场，黑色实心点代表稳定平衡点，空心点代表不稳定平衡点，（C）分岔图

更复杂的是跨临界分岔，它不产生或消灭平衡点，而是让两个已有的平衡点在相遇时交换稳定性。最富戏剧性的是叉形分岔，它常见于具有对称性的系统。它又分为两种截然不同的类型，超临界叉形分岔：当参数越过临界点，中央的稳定态失稳，系统发生对称性破缺，会平滑地、选择性地进入两侧两个新的稳定态之一。在临界点附近，系统恢复力会变得极弱，出现临界慢化现象。亚临界叉形分岔：这则是一个陷阱。在中央稳定态失稳前，两侧早已潜伏着不稳定的分支。一旦越过临界点，系统不会进入新的稳定态，而是会“爆炸”式地逃离，发生有限时间逃逸，其后果往往是灾难性的。如图2所示。

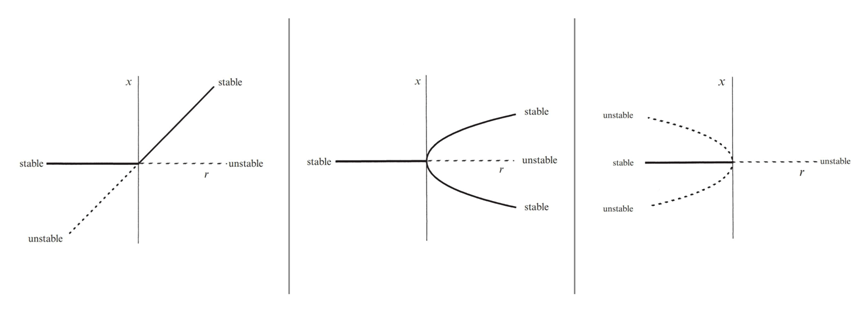
图2：从左到右，依次为跨临界分岔图，超临界叉形分岔图，亚临界叉形分岔图。

然而，现实世界比这些单参数模型更复杂。如果系统由两个参数控制（即系统的余维数为2），我们会观察到更奇异的行为，比如尖点分岔，如图3所示，这个动力系统的状态在某一区域折成上下两层，从侧面看（投影）就出现分叉曲线。当外部条件（如图中的h）慢慢变化、状态点沿上层走到折边尽头时，它会突然跳到下层，此时就会出现滞后分叉；但如果是固定h，而调节r的话，则会出现我们刚才提到的超临界叉型分叉。尖点分叉很好地将两种不同的分叉统一在一个图像当中，可以用来建模更复杂的突变行为。

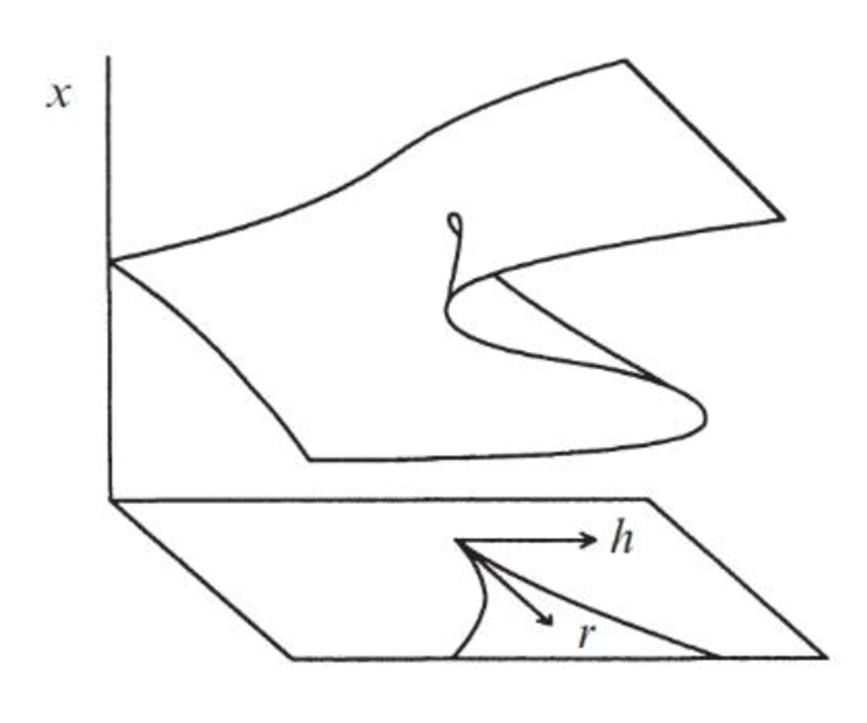
图3：尖点分岔示意图

而联系物理系统，尖点分岔能很好地帮助我们理解物理学中铁磁系统与气液系统的性质：将如图3所示的尖点分岔的三维折叠向三个平面投影，获得的结构和气液系统与伊辛铁磁体系统的相图惊人地如出一辙（如图4所示）。而杨振宁先生与李政道先生关于磁性格气的工作，恰好在铁磁系统和气液系统之间架起了一座数学的桥梁，严格证明了二者的等价性。这让我们意识到我们在铁磁系统和气液系统中观察到的相变行为，其背后的数学结构来自于突变理论。

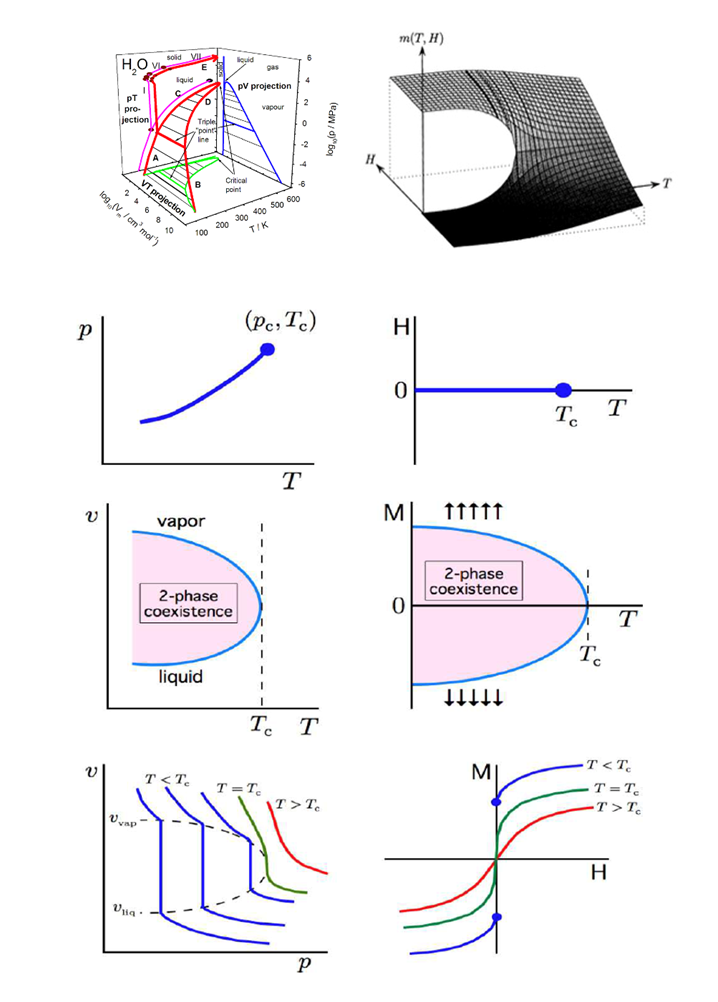
 图4：左边为气液相图，右边为伊辛铁磁体相图，最上面两个图分别为水的三维相图和 Ising模型的三维相图，下面六个图为三维相图在不同面上的投影

法国数学家、菲尔兹奖得主勒内·托姆在20世纪60-70年代创立“突变论”（新三论之一），是分岔理论的自然发展。他将目光投向了所有这类光滑、连续的参数变化导致的分岔，并证明，当控制参数（余维数）不多于四个时，所有可能的“突变”类型只有七种基本类型，即七种初等突变，如图5所示。我们最初讨论的鞍-结点分岔，是余维数为1的突变；而尖点分岔，是余维数为2的突变。此外，还有燕尾、蝴蝶、椭圆脐点等充满诗意的名字，它们共同构成了数学家为自然界一切“突然的断裂”所绘制的终极地图。

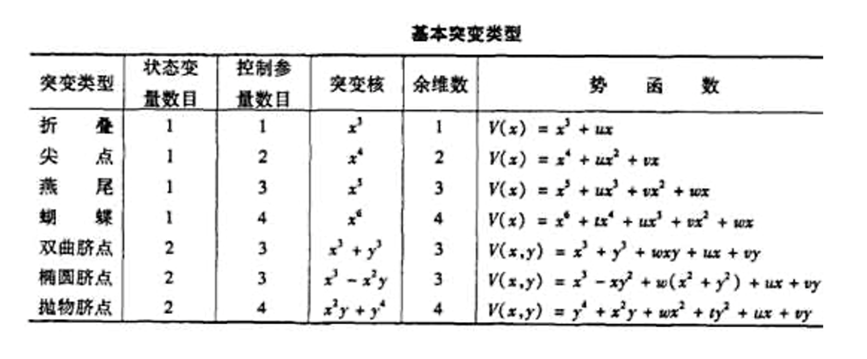
图5：七种基本突变的分类，展示其对应的维数、余维数和势函数

从数学上看，分岔理论为相变临界现象提供了严谨的拓扑学和动力学基础。它告诉我们，系统在临界点附近的行为遵循着由系统内在结构决定的特定分岔模式，其类型由系统状态变量的维数和控制参数的维数共同主导。物理学的相变和数学的分岔，如同两条从不同源头出发的河流，此刻正奔向同一个交汇的海洋。

统一的语言：从相变、分岔到临界点

那么，物理学的相变（和临界）与数学的分岔（和突变）的统一描述是怎样的？分岔是确定性动力系统的结构稳定性问题，而统计物理中的热力学相变，可以看作是一类随机动力系统的结构稳定性问题。

经典的平衡态统计物理处理的，正是包含亿万个粒子的系统。这种巨大的自由度，使得我们无法精确追踪每个粒子，只能用概率和统计来描述。这本质上就是一种随机动力系统——在平衡态的框架下，我们发展出了气体动力学、近独立子系统计等理论，特别是针对可以写出哈密顿量的系统，19世纪末20世纪初，科学家建立系综理论，在这一框架下，我们可以直接考察平衡态系统的相空间中的状态分布。但如果我们考察这样的系统对应的非平衡动力学，比如写出对应哈密顿量的过阻尼朗之万方程，我们便马上会意识到这就是一个含有噪声的随机动力系统。因此，正如平衡态统计物理只是在处理一类随机动力系统的统计性质，相变与分岔在精神内核上也是统一的，都是关注于动力系统相空间的不变集的拓扑结构的变化。

这个统一的视角，为我们理解复杂系统中的临界点（tippingpoint，见注1）提供了强大的理论武器。然而，真实的复杂系统中，如社会、生态和气候系统等，存在着多种多样的临界点，其噪声形式、分岔类型远比上一节确定系统的分类更为丰富和微妙。那么我们能否给出一个更广泛的框架，用于统一描述这些临界点呢？

注1：临界在不同语境下，具有不同的含义。在热力学和统计物理的语境下，Critical transition，翻译为临界相变。在一般的复杂系统中，Tipping point，翻译为临界点，它的含义更广，可以考察非平衡系统的结构稳定性问题。

近年来，科学家们正努力建立一个更普适的理论框架，将Bifurcation-induced-tipping（分岔诱导突变）、Noise-induced-tipping（噪声诱导突变）和Rate-induced-tipping（速率诱导突变）等不同类型的突变统一在同一个语言体系下。这个框架的核心思想，是关注系统内部存在的多个参数的对应时间尺度的相对性，这也是托姆的突变论的自然推广。我们考虑这样的一个随机动力系统，如图6所示：

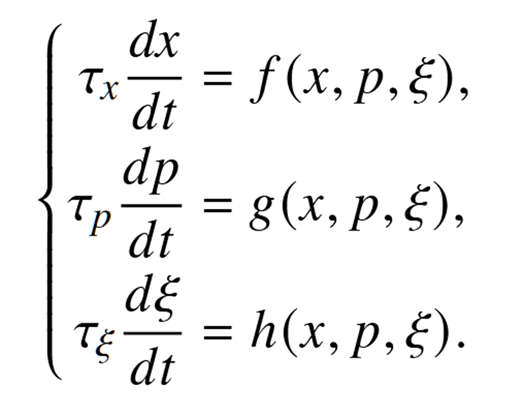
图6：随机动力系统。来源： 马智钦，预测非线性随机系统的临界转变:  模型和数据驱动方法研究

其中是状态变量，是系统参数，是随机变量（噪声），是3种相对时间尺度。具体为：

1.：系统在受到小扰动后，依靠系统本身恢复到平衡态所需的时间。

2.：外部控制参数发生显著变化所需的时间。它代表人类活动或自然过程驱动系统变化的速度，例如大气二氧化碳浓度上升至新水平所需的时间。

3.：随机扰动（即噪声）的持续时间。它量化了环境中不确定性的活跃程度，例如环境噪声的特征时间。

当时，外部参数变化极其缓慢，系统有充足时间适应并跟踪每一个微小的变化；而噪声变化又如此之快，其影响在统计意义上被平均掉了。此时，我们的动力系统就优雅地退回到经典的分岔和突变理论，可以按照维度n和余维度m进行像勒内·托姆那样的分类。这正是B型临界（B-tipping）。

因此，通过分析这三个时间尺度的相对关系，我们可以找到更多更符合实际的临界类型：

N 型临界 (N-tipping)：当 时，系统虽然稳定，但距离分岔点已经很近，持续的随机噪声将使系统逐渐偏离平衡区。此时，中等强度的随机噪声 ξ 就可能成为“临门一脚”，触发tipping的发生。甚至，系统会在新旧状态附近“闪烁”（flickering），频繁地在两个状态之间跳跃。例如在洱海等生态系统中观察到，它在“草型清水稳态”和“藻型浊水稳态”两种状态间转换。

R 型临界 (R-tipping)：当 时，系统面临的是一个完全不同的问题。外部参数 p 的变化速度太快，系统内部的动态过程 x 根本来不及跟上参数的变化系统，因而未能追踪连续变化的吸引子。即使最终的参数值 p 本身位于一个稳定的区域内，系统也可能因为“追不上”而崩溃。例如典型的堆肥炸弹模型，在西伯利亚泥炭/永冻土区，若大气升温的速率过快，土壤呼吸迅速增强并放热，进一步升高土温，形成“升温→呼吸增强→再升温”的正反馈；系统“追不上”移动的稳定态，突然跃迁至高温高排放态，出现土壤温度失控上冲与大规模碳释放的“堆肥炸弹”不稳定性。

物理学把“相变”从经验观察推进为可计算的问题，分岔与突变理论用动力系统的语言描述稳定状态如何更替。两条路线共同指向“结构与稳定性的变化”，构成了一个既能证明、也能分类的框架。通过这样的统一定义和分类，我们就更加深刻地理解了不同类型临界之间的关系，这为我们关注具体某个系统中的临界现象打下了坚实的理论基础。

作者：邱仲普 

审核：樊京芳 北京师范大学系统科学学院教授、院长

出品：中国科协科普部

监制：中国科学技术出版社有限公司、北京中科星河文化传媒有限公司

来源: 科普中国创作培育计划

内容资源由项目单位提供